|
|
Section 5.2
Finding Forces on Welds
Last Revised: 07/08/2023
Now that you know a little about welds and what they do, let's look at ways in which we can determine the force on a part of a weld in a connection. The methods and procedures commonly used for finding forces resulting from applied forces are presented below. Note that these methods and procedures result from principles of structural mechanics and structural analysis and are NOT found in the specification. As far as the specification is concerned, it is the engineer's responsibility to find the forces in welds by any defendable method.
It is common to express the results of weld force calculations in terms of the force per unit length of weld. In connections where there is eccentricity, the stress varies throughout the weld group. The force per unit length is found by multiplying the stress (force per unit area) at a given location by the effective throat (or weld thickness), te, at that location.
Connections with Concentric Forces
|
Figure 5.2.1 |
|
Figure 5.2.1 illustrates two connections where the applied force, P, is concentric with the fillet weld group.
In each case, the stress at any location equals the concentric force, P, divided by the area of the welds (sum of tel for all weld segments).
Note that, for fillet welds, we do not differentiate between tensile and shear force. In a fillet weld all stresses are assumed to be shear as they will have a significant shearing component on the critical face of the weld.
An important assumption when determining the shear in welds WHERE THE APPLIED CONNECTION FORCE IS CONCENTRIC WITH THE WELD GROUP is that all shear planes in a connection see the same applied shear STRESS, fv. This is an appropriate assumption because all welds are constrained by the connected members to deform the same. If they all have the same shear deformations, then they all have the same shear strains and hence they all have the same shear stress.
The shear stress, fv, on the critical shear planes equals the total force being transferred divided by sum of all the shear plane areas:
fv = P / S(Shear Plane Areas) = P / S(te * lengths)
The UNIT SHEAR FORCE = fv te (units are force per unit length of weld)
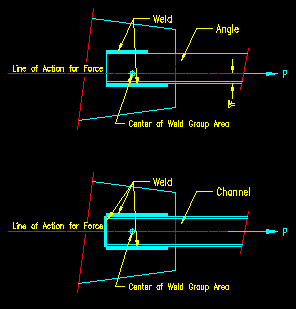
In Plane Eccentrically Loaded Connections
As with bolts, there is an elastic method based on basic principles of superposition and there is an ultimate strength method that looks at the simultaneous translation and rotation of the connection. Additional, new with the 15th edition and continued in the 16th edition, is a plastic method. All three are found in the welding section of the SCM (part 8, pages 8-13 to 8-19). Figure 5.2.2 depicts a typical case of an eccentrically loaded weld group, with the load in the plane of the faying surface.
Figure 5.2.2
Eccentricity in the Plane of the Faying Surface
Click on image for larger view
The Elastic Method
The Elastic method is described in the SCM starting on page 8-15. Using the principle of superposition, the applied forces are converted to a concentric (i.e., passes through the center of the weld group) translational force and a rotational moment.
The stress due to the translational force is equal to the applied force divided by total length of the weld and effective throat, te. See SCM page 8-15 for the equations. The direction of the reactionary stress is opposite that of the applied force. It is common practice to break the force into orthogonal components (i.e., in the "x" and "y" directions, as shown in Figure 5.2.3) and combine the stresses vectorally with the stress resulting from the moment.
Figure 5.2.3
Translational Forces and Reaction Stresses
Click on image for larger view
Note that the orientation of the weld with relation to the direction of the applied force is not of concern. All the stresses are assumed to be shear stresses.
The stress due to the applied moment is determined using the torsion formula learned in Mechanics. The equation can be found on SCM page 8-15. Figure 5.2.4 shows the applied force and the reactionary stresses. Note that the stress at any location is perpendicular to a line from that same location that passes through the center of gravity of the bolt group.
Figure 5.2.4
Rotational Force and Reaction Stresses
Click on image for larger view
Computing the stress due to the applied moments requires that the polar moment of inertia be computed for the weld group. SCM page 8-16 gives some equations for Ix and Iy for some common weld shapes. Using the parallel axis theorem, these equations can be combined to find Ix and Iy for the group relative to the weld group centroid. With this information Ip can be computed since Ip = Ix + Iy.
From the given equations the stresses at any point in the weld group can be determined by vectorally adding the translational and rotational components for the stresses at the point of interest. SCM page 8-15 provides general equations for determining the two orthogonal components of the rotational reaction and how to vectorally add the components together.
As stated above, the goal is to find the largest stress, fv, in the weld group.
The maximum stress can then be expressed as a unit shear force:
The UNIT SHEAR FORCE = fv te
The Instantaneous Center of Rotation (aka Ultimate Strength) Method
|
Figure 5.2.5 |
As with bolts, the Elastic Method is conservative and inconsistent with test results. The IC method is more consistent with test results because it takes into account the simultaneous translation and rotation, without superposition, of the loaded connection. The method is presented in the SCM starting on page 8-13.
The IC method for weld groups follows the same principles used for the IC method for bolt groups. The main difference between the two methods is that welds tend to be continuous and there is a different load-deformation relationship. Figure 5.2.5 gives the basic geometric quantities that will be used in the following description of the method.
The IC method for welds begins with dividing the weld into discrete elements. These discrete elements are treated similar to the bolts previously described in chapter 4 of this text. As with all discrete approximations, increasing the number of elements increases the accuracy of the results. Twenty elements seem to give good results for most connections.
The load-deformation relationship (SCM equation 8-3) for welds is given on SCM page 8-13. This relationship approximates the load-deformation test data. As can be seen from SCM Figure 8-6, the load-deformation relationship changes with the angle between the axis of the weld and the direction of the reaction force in a manner that is consistent with the discussion given in BGSCM 5.5. The computation of the angle of load to weld axis complicates the load-deformation computation somewhat, as this angle must be determined for each element of weld.
The load-deformation equation given on SCM page 8-13 results in a quantity that is in terms of stress. To obtain the load per unit length of weld the result of the equation must be multiplied by the weld effective throat, te.
It appears that the SCM presentation on the IC method is not very complete. In the SCM 14th edition additional information was available in SCM J2.4(b). That information was not found in the SCM 15th edition. It is not in the SCM 16th edition either.
The basic approach is to divide the weld groups into small elements, determine which element is the critical element (i.e., the one that will "fail" first), using the critical element, get the the deformations in all the other elements as a ratio of their distance from the IC, use the load/deformation relationship to get the stress in each element, compute the force in each element, then use equilibrium equations to determine if the right IC has been found. Repeat the procedure until the equilibrium equations all agree. The resulting Pn is the capacity of the weld group for the given location and direction of applied force. One of the example problems will demonstrate the method.
Based on SCM 14th edition J2.4(b) and the explanation in Part 8 the method for computing the force in each of your weld elements goes something like this:
- You will need to know the configuration of your weld group and its
geometric relationship to the line of action of the applied force.
- You need to choose a location for the I.C.
- You will need to compute component distances (i.e., parallel to the
reference coordinate system axis) to the center of each of your weld
elements from the IC. This allows you to compute distance of the
element from the I.C. (ri) and the angle relative to the
reference coordinate system (di) and
the angle between the weld axis and the resultant force on the weld element
(qi). Keep in mind that the
force on weld element is perpendicular to the radius line from the element
to the I.C.
- At this point you can compute the deformation of each element at
ultimate stress, Dui.
Dui = min[1.087(qi + 6)-0.65 a, 0.17a]
- The critical element will be the one with the lowest
Dui/ri
ratio. This is normally the element furthest from the I.C. but not always. The "r" of this critical
element becomes rcr and the deflection of this critical element
is taken as Ducr. The critical ratio can be expressed as:
(Ducr/rcr) = min (Dui/ri)
- As the deformations are assumed to be proportional to the
element distance from the I.C. we can find the deflections in each of the
elements when the critical element is at ultimate stress by:
Di = ri * (Ducr/ rcr)
- You then need to determine the deformation in each element at its maximum possible stress. This quantity is needed for the load/deformation relationship equation. To do this we find the deformation using the equation:
- We can now compute the ratio of the ith element's deformation to its own deformation at maximum stress:
- We can now compute the stress in each weld element using the SCM load/deformation relationship equation 8-3 as follows:
- With the stress in each weld element, you can now compute the magnitude of the force, R, on each element by multiplying Fnwi by the effective area, Awei, of each element:
- Recalling that these element forces are perpendicular to their radial from the IC, the forces can then be broken into their horizontal and vertical components for use in the equilibrium equations as follows. This is similar to how we dealt with the bolt forces when applying the IC method to eccentrically loaded bolted connections:
Dmi = 0.209(qi
+ 2)-0.32 a
pi = Di /
Dmi
Fnwi = 0.6FEXX(1.0 + 0.5 sin1.5qi)[pi
(1.9 - 0.9pi)]0.3
Ri = Fnwi * tei Li
= Fnwi * Awei
Rix = Ri sin di
Riy = Ri cos di
SFx = 0 =
SRix - Pnx =
S(Ri (riy / ri)) - Pn
sina
Pn = S(Ri (riy
/ ri) )/ sina
SFy = 0 =
SRiy - Pny =
S(Ri (rix / ri)) - Pn
cosa
Pn = S(Ri (rix
/ ri)) / cosa
SM = 0 = S(Ri
* ri) - Pn ro
Pn = S(Ri * ri)
/ ro
The above equilibrium equations are useful in finding the proper IC. Since all the radial distances and angles are functions of the location of the IC, coordinate values of the IC are iteratively selected until equilibrium is satisfied (i.e., when all the equilibrium equations yield the same Pn). This procedure is well suited to a spreadsheet using an optimization routine such as the “solver” found in MS Excel.
The resulting Pn is the nominal capacity of the weld group.
The AISC Coefficient Method
Similar to the method provided for bolts which was discussed in BGSCM 4.3, AISC has solved the IC method for many situations and has provided tables with the resulting coefficients. These begin on SCM pg 8-71. These extensive tables do not begin to cover all possible cases so there will be times when you need to compute your own coefficients.
Take some time to look at SCM Tables 8-4 through 8-11 to see how to determine C for a given situation. Note that there are tables for a wide variety of weld configurations and load scenarios, however they do no cover every situation and it is frequently necessary to interpolate between published values or even resort to solving the IC problem on your own.
You will need to examine the variables in each table to see how they are applied. There is some variation from table to table. Generally, you will need to compute values of 'k' and 'a' to use the tables. For a given weld configuration, you know the values for 'kl' and 'al' ('kl' is the distance between welds or the length of a leg as defined on the appropriate sketch and 'al' is the eccentricity distance ex as defined on the appropriate sketch).
k = (kl)/l
a = (ex)/l = (al)/l
The conditions given on SCM pages 8-71 through 8-76 are unique in that they can also be used for out-of-plane eccentricity by setting k equal to zero. This is a very common situation--particularly for beam connection tabs.
As we have seen, C relates the force in a weld to the overall force on the connection. The use of these tables is self-explanatory. Spend some time reviewing them.
The Plastic Method
On SCM page 8-17 a method known as the Plastic Method is presented to deal with a special case of out-of-plane eccentricity. The method deals with the very common special case of a pair linear welds subject to an out-of-plane eccentric load (Table 8-4 for the k=0 case, if using the AISC coefficient method). The revised method in the 16th edition is an improvement over the procedure originally presented in the 15th edition.
In this method the required weld size is determined using weld geometry and loading. SCM equations 8-23 are used to determine the weld size. The equations are dependent on a the term Nequiv.
Two approaches are presented for determining the term Nequiv used in the weld size determination: the Conventional Plastic Method (CPM), and the Optimum Plastic Method (OPM). The CPM is the simpler of the two methods and is considered to be more conservative. Neither of the methods are computationally complex.
In the CPM, the full length of the weld is used to resist the bending and normal forces, as shown in SCM Figure 8-9(a). For the CPM, the equation for Nequiv is given in SCM Equation 8-27a. The equation is quite simple.
The OPM can only be used when the normal force, Nr, is not zero. The assumed stress distribution is more complex than that used in the CPM and equations 8-27b and 8-28 are provided to compute Nequiv.
The procedure appears to be set up for 70 ksi electrodes. It may be possible to use the coefficients found in SCM Table 8-3 to adapt to other electrode strengths, however this is not mentioned in presentation of the Plastic method.
Eccentricity Normal to the Plane of the Faying Surface
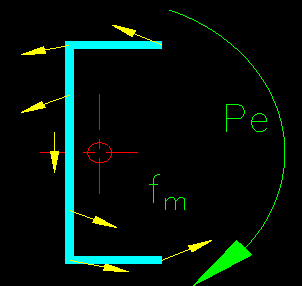
The SCM presents an elastic method for determining the stresses in welds when the eccentricity is normal to the plane of the faying surface (see SCM page 8-12). The SCM discussion is pretty sparse but adequate. The basic approach is an elastic vector approach where the force is moved to be concentric with the weld group and a moment added account for the bending resulting from eccentricity. Figure 5.2.6 illustrates the condition.
Figure 5.2.6
Eccentric Load Out-of-Plane of Faying Surface
Click on image for larger view
The basis of the method is founded in principles of elastic mechanics. Use is made of the principle of equivalent forces and basic concepts of stress.
The force is moved so that it passes through the center of the weld group at the faying surface and the corresponding moment (Pe) is applied about the neutral axis of the weld group.
The forces are considered to be resisted by the weld group without taking into consideration any contribution from the compression between the connected parts.
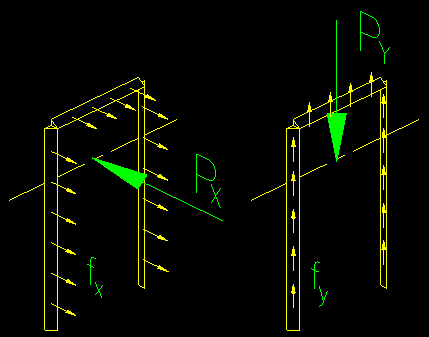
The stresses are computed using basic principles of mechanics. The translational stresses are shown in Figure 5.2.7.
Figure 5.2.7
Translational Forces and Reaction Stresses
Click on image for larger view
The stresses are computed using the equations:
fx = Px / Aw
fy = Py / Aw
Where:
- Px = the component of P normal to the faying surface
- Py = the component of P parallel to the faying surface
- fx = normal stress in the lateral direction
- fy = normal stress in the vertical direction
- Aw = effective area of the weld group (SteLw)
- te = The effective throat of the weld
- Lw = length of weld segment of effective throat te
The stress due to the rotational force are depicted in Figure 5.2.8.
Figure 5.2.8
Rotational Force and Reaction Stresses
Click on image for larger view
The stresses are computed using the bending stress equation:
fb = Pe c/Iw
Where:
- Pe = the applied moment
- c = maximum distance from the neutral axis. For this problem we are only interested in the tension stress, so it is the distance from the neutral axis to the furthest weld in tension.
- Iw = the moment of inertia of the weld group about the centroidal axis.
The resultant maximum stress is the vector sum of the three stress components.
![]()
Multiplying fmax by te gives the maximum unit force applied to the weld group. The resulting unit force is then compared to the capacity (frn or rn/W, depending on whether P was Pu or Pa).
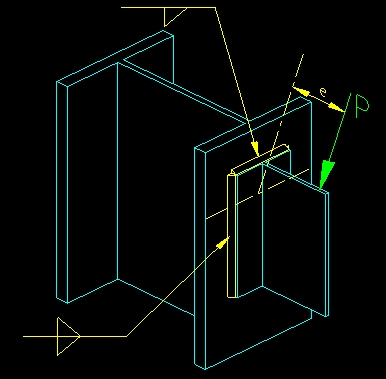
An example of a connection with an out-of-plane eccentricity is shown in Figure 5.2.9.
Figure 5.2.9
Seat Connection
Click on image for larger view