|
|
Section 9.4
SCM Appendix 8 Second-Order Effects
Last Revised: 05/21/2023
The SCM approach for magnifying moments and axial forces derived from a first-order analysis for second-order effects is found in SCM Appendix 8. This section can be used to perform approximate second-order analysis on the results of first-order elastic analysis done when using either the Direct Analysis or Effective Length methods. In this section, the magnified moments and forces are referred to as "required strengths" and have the subscript "r". There is no need to use this procedure if the structural analysis in either method incorporated a second-order analysis.
It is common to perform the analysis without considering second-order effects. When this is the case, separate analyses (see BGSCM 9.3) must be performed for cases where lateral movement is restrained and where lateral movement is unrestrained.
Moments and axial forces that result from an analysis that does not permit joint translation are given the subscript "nt" for no translation. Moments and axial forces that result from joint translation are given the subscript "lt" for lateral translation and are found by taking the difference between the internal forces from the unrestrained analysis and the internal forces resulting from the restrained analysis.
The General Equations
SCM equations A-8-1 and A-8-2 give equations for amplified required moment and axial force. The equations combine the amplified effects resulting from the two separate analyses.
A point to emphasize is that, though the components come from two separate analysis, they are SIMULTANEOUSLY OCCURRING AT THE SAME LOCATION AND IN THE SAME PLANE. Do not mix moments from different points on the member!
B1 is the amplifier for moments resulting from the analysis of the member restrained against joint translation. The equation (SCM equation A-8-3) for B1 includes a term, Cm, to estimate relative magnitude of the deflection, d, between the joints.
The maximum value of Cm is 1.00 and can be conservatively taken as such in any case. However, when maximum member moment occurs at the joints and the moment is non-uniform (it is linear!) along the member, it is reasonable to assume that d is smaller than would be otherwise predicted from the end moments. The factor Cm accounts for this behavior.
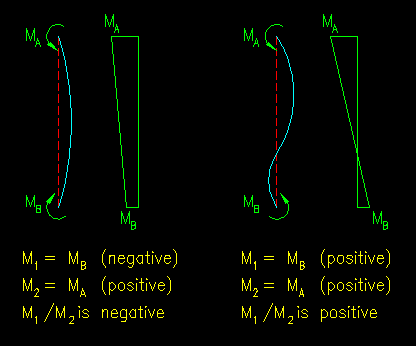
The equation for Cm (SCM equation A-8-4) includes terms for the end moments, M1 and M2, which are defined as the smaller (smallest absolute value) and larger end moments, respectively. If, on a free body diagram, the signs are kept true to the right-hand rule, the ratio of M1 to M2 will be negative if the member is in single curvature and positive if in reverse curvature as shown in Figure 9.4.1.
Figure 9.4.1
Computation of M1/M2
Click on image for larger view
The equation for B1 include a term (Pe1) for the Euler buckling load for the column in the plane of buckling/bending that is under consideration. When computing Pe1, the value of K used to compute Lc1 is to assume that there is no joint translation for the column--in other words, as if the column is part of a braced frame.
The factor B2 considers the effect of joint translation. In building structures, the ends of columns in a given level are all generally restrained by floor structures at each end. This requires all columns in the level to move together for the case of joint translation. Consequently, the equation for B2 effectively considers the entire story as a column. The terms in SCM equation A-8-6 include the force transferred through the story (Pstory) as well as the total buckling strength of the story (Pe story). While it is relatively easy to compute Pstory, Pe story is different.
In versions of the specification before SCM 14th edition, B2 could be computed by summing the buckling strengths of all the columns in the direction under consideration. That is no longer an option in the SCM. What remains is a computation based on an analysis of the structure which yields the first-order story drift, DH, plus the story shear, H, and the vertical load transferred by moment frames, Pmf. The procedure in SCM Appendix 8 is a modification on the procedure presented in editions of the SCM prior to SCM 14th edition. You will want to take some time to read the details of SCM Appendix 8.2.2 to get the details not covered here.
It is important to note that the story deformation, DH, is a function of the bending stiffness of all the columns in the level contributing to lateral stiffness of the structure in the plane under consideration. Consequently, the second-order effects of all the columns in the level are interrelated. Also, changing even one column size will change DH so the design process is likely to be iterative until it can be shown that all columns on the drawings satisfy the requirements.
Again, recall that everything done in these analyses is IN A PLANE. Consequently, when computing the Pe2 for each column, if the column orientations change in the level, some columns Pe2 will be strong axis dependent and some weak axis dependent.
Note that the magnifiers, B1 and B2, are never to be taken as less than 1.00. A value of less than 1.00 suggests that the axial compression reduces the first-order moments. This cannot be true, hence the SCM limit on B1 and B2.
Once the magnifiers, B1 and B2, are determined then the axial forces and moments are recombined using SCM equations A-8-1 and A-8-2 to obtain the required axial force, Pr, and required moments, Mr, for use in the combined force equations of SCM Chapter H.