|
|
Section 3.7
Block Shear Rupture
Last Revised: 01/14/2013
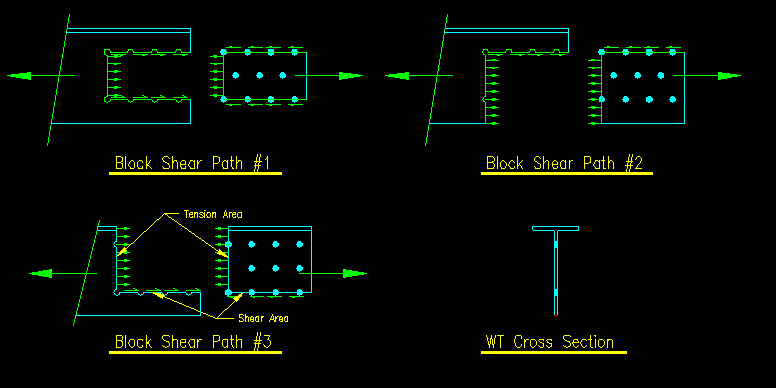
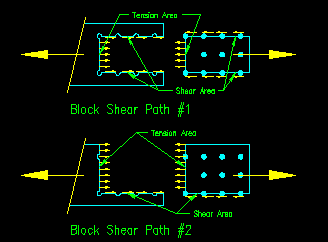
Block shear is, in some ways, similar to tensile rupture in that the main part of the member tears away from the connection. The provisions for block shear are found in SCM J4.3 (SCM page 16.1-129). The difference is that there is now a combination of tension and shear on the failure path. Like tensile rupture, there frequently is more than one failure path. Figure 3.7.1 shows three possible block shear failure paths for a WT section.
|
Figure 3.7.1 |
|
|
The Limit State:
The basic limit state follows the standard form. The statement of the limit states and the associated reduction factor and factor of safety are given here:
| LRFD | ASD |
| Pu < ftRn | Pa < Rn/Wt |
| Req'd Rn = Pu/ft < Rn | Req'd Rn = Pa Wt < Rn |
| Pu / (ftRn) < 1.00 | Pa / (Rn/Wt) < 1.00 |
| ft = 0.75 | Wt = 2.00 |
The values of Pu and Pa are the LRFD and ASD factored loads, respectively, applied to the member.
Nominal Block Shear Rupture Strength, Rn:
The limit state value computed is the force that STARTS the rupture. Historically, the SCM equations have assumed that rupture initiates either on the tensile area(s) or on the shear area(s), not on both surfaces simultaneously. With the AISC specification found in 13th edition of the SCM, revised equations were introduced. The new equations continue in the 14th edition (Equations J4-5, in SCM J4.3). You should also read the commentary on the section (SCM pg 16.1-411).
The basic concept for computing the block shear rupture strength is that we compute the strength of the tension region and the strength of the shear region and add them together. If you look at SCM equation J4-5 you will see the two terms. SCM equation J4-5 computes the nominal resistance, Rn, or strength associated with block shear.
You should also notice that there are actually two equations in equation J4-5. The term to the left is the situation for shear rupture/tensile rupture and the equation to the right is for shear yielding/tensile rupture. The way the equations are written, you compute both values and take the smaller of the two.
One thing that you might notice right off is the presence of a "0.6" in the shear terms. It turns out that the Fu and Fy values are determined by tension tests. The comparable terms in shear are approximately 0.6 times the values for tension. Consequently, wherever shear strength is computed, we use the tension values multiplied by 0.6. Chances are, whenever you see 0.6Fy and 0.6Fu in an equation then that equation is computing shear strength.
The other quantity that will be new to you is the Ubs quantity. Ubs was new with the 13th edition and continues in the 14th edition. This quantity is used to account for non-uniform tensile stress distribution when the block shear region is non-symmetric or in any other case where non-uniform tensile stress is likely to occur on the tensile fracture area. This condition generally occurs whenever there is only one shear area in the failure path. The SCM commentary gives examples of such situations (SCM page 16.1-412). We have this situation in our example problem 3.1.
Equation J4-5 also contains three area quantities: Agv, Ant, and Anv. These terms are defined in SCM J4.2 and SCM J4.3 and represent the gross and net areas in tension and shear along the failure path. The same concepts dealing with holes that we discussed under tensile rupture apply to the computation of these quantities as well.
Comparing the two failure paths, the second path is the controlling path because it yields the lesser value.See example problem 3.1 for implementation of this limit state.
Another Example:
Example 3.1 is not sufficient to show what would happen with a flanged member, so let's assume that a W10x30 is used to replace the tension member used in example problem 3.1. The same bolt pattern and size is to be used. The same steel is also used. The same two failure paths are potentially a problem. Compute Rn for each path.
For failure path #1, the only difference to the prior calculation is that the plate thickness is now the thickness of the web, tw, for the given section. The values for the areas previously computed for path #1 can be multiplied by (tw/0.75") to get the new values (the areas are linear with plate thickness in this case).
Agv = (15.75 in2)(0.30"/0.75") = 6.300 in2
Anv = (11.16 in2)(0.30"/0.75") = 4.46 in2
Ant = (3.84 in2)(0.30"/0.75") = 1.54 in2Rn = (563.1 k)(0.30"/0.75")
Rn = 225.3 k
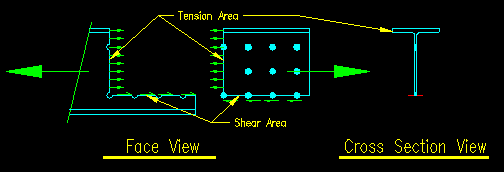
The big difference comes in path #2. In this case, the added tension area picks up the area of a flange when the path exits to the side of the member. This makes Ant very large for failure path #2. Figure 3.7.2 shows the cross section for Ant.
Figure 3.7.2
Tension Area
Agv = (7.875 in2)(0.30"/0.75") = 3.150 in2
Anv = (5.58 in2)(0.30"/0.75") = 2.231 in2
Ant = (half Ag of section) + 3"(tw) - (1.5 holes in the web) = 4.926 in2
Rn = 1027 k not to exceed 665 k = minimum(1027 k, 665 k)
Rn = 665 k
In this case, failure path #1 controls since the tension area in failure path #2 more than compensates for the loss of shear failure path from path #1. The added flange area makes a big difference! Most experienced engineers would probably have skipped failure path #2 because of this.
Sample Spreadsheet Pn Computation
There are probably many ways to arrange this computation, but here is one. The values in the shaded cells are either entered manually or computed elsewhere and linked to these locations. Note that this spreadsheet only ANALYZES a given member. For design problems where the member is unknown, you will need to solve the limit state equation for the required bolt hole spacing and end distance then make decisions from there. In the end, however, you need to show that your final selection satisfies the limit state using some calculation similar to the one shown here.
| Block Shear (SCM J4.3) | Rn = min[0.6FuAnv + UbsFuAnt, 0.6FyAgv + UbsFuAnt] | |||||||
 |
||||||||
| Fy = | 36 | ksi | ||||||
| Fu = | 58 | ksi | ||||||
| tpl = | 1 | in | ||||||
| db = | 0.75 | in | ||||||
| Failure Path #1 | gross path | number | net path | |||||
| length | holes/path | length | # paths | Area | ||||
| (in) | (in) | (in^2) | ||||||
| Agv | 10.500 | 0.000 | 10.500 | 2.000 | 21.000 | |||
| Anv1 | 10.500 | 3.500 | 7.438 | 1.000 | 7.438 | |||
| Anv2 | 10.500 | 3.500 | 7.438 | 1.000 | 7.438 | |||
| Ant | 6.000 | 1.000 | 5.125 | 1.000 | 5.125 | |||
| Ubs | 1.0 | |||||||
| Shear | Shear | Use | ||||||
| Fracture | Yield | |||||||
| (k) | (k) | (k) | ||||||
| Rn | 814.9 | 750.9 | 750.9 | |||||
| Failure Path #2 | gross path | number | net path | |||||
| length | holes/path | length | # paths | Area | ||||
| (in) | (in) | (in^2) | ||||||
| Agv | 10.500 | 0.000 | 10.500 | 1.000 | 10.500 | |||
| Anv | 10.500 | 3.500 | 7.438 | 1.000 | 7.438 | |||
| Ant | 7.500 | 1.500 | 6.188 | 1.000 | 6.188 | |||
| Ubs | 0.5 | |||||||
| Shear | Shear | Use | ||||||
| Fracture | Yield | |||||||
| (k) | (k) | (k) | ||||||
| Rn | 452.8 | 420.7 | 420.7 | |||||
| Controlling Rn = | 420.7 | k | ||||||
| IF you need to determine capacity: | ||||||||
| LRFD | ASD | |||||||
| ft = | 0.75 | Wt = | 2 | |||||
| ft Pn = | 315.5 | kips | Pn / Wt = | 210.4 | kips | |||
| CLF | 1.40 | CLF | 0.90 | |||||
| Ps,eq = | 225.4 | kips | Ps,eq = | 233.7 | kips | |||
| If you need to check capacity: | ||||||||
| LRFD | ASD | |||||||
| ft = | 0.75 | Wt = | 2 | |||||
| ft Pn = | 315.5 | kips | Pn / Wt = | 210.4 | kips | |||
| Pu | 50.00 | kips | Pa | 50.00 | kips | |||
| Pu/ftPn = | 15.8% | kips | Pa / (Pn / Wt ) = | 23.8% | kips | |||
| Okay | Okay | |||||||