|
|
Section 3.3
Tensile Yielding of a Member
Last Revised: 11/04/2014
Tensile yielding is the first of the strength based limit states that we consider in this text. As you will recall from your mechanics course, the stress and strain in a tension member, away from end connections, is assumed to be uniform throughout the member as long as the force is concentric with the member. For a tension member, this means that the entire member can yield and experience permanent elongation if the force in the member is high enough. Permanent deformation is not a desirable state, so the limit state of tensile yielding is introduced to guard against this form of "failure" to satisfy the needs of the structure.
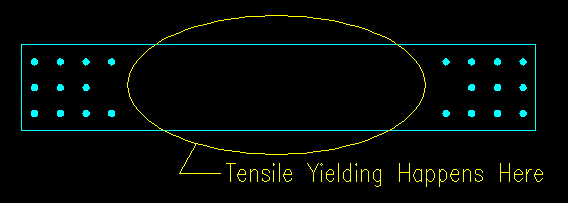
Tensile yielding is considered away from the connections in the mid part of the member. Figure 3.3.1 shows the general region of concern for a flat plate member.
|
Figure 3.3.1 |
|
|
SCM D2 contains the limit states for tensile yielding and tensile fracture. The two together are known as tensile strength. In this section, we will look at only tension yielding.
The Limit State:
The basic limit state follows the standard form. The statement of the limit states and the associated reduction factor and factor of safety are given here:
| LRFD | ASD |
| Pu < ftPn | Pa < Pn/Wt |
| Req'd Pn = Pu/ft < Pn | Req'd Pn = Pa Wt < Pn |
| Pu / (ftPn) < 1.00 | Pa / (Pn/Wt) < 1.00 |
| ft = 0.90 | Wt = 1.67 |
The values of Pu and Pa are the LRFD and ASD factored loads, respectively, applied to the member. In this case Pn is the nominal tensile yielding strength of the member.
Nominal Tensile Yielding Strength, Pn:
Pn is computed using SCM equation D2-1 and is in force units. As you will recall from mechanics, for an axial force member, the force in the member equals the normal stress times the cross sectional area of the member. In this case, we multiply the gross cross sectional area, Ag, by the yield stress, Fy to determine force that would cause the member to yield in tension.
The maximum force a member can resist is commonly referred to as the STRENGTH of a member.
As shown in the SCM overview given in chapter 1, the values for Fy and Fu can be found in SCM Tables 2-4 through 2-6 as appropriate.
Ag is the gross cross sectional area of the member and is defined in SCM section B4.3a. You should read that section now. This area is normal to the axis of the member. Ag is tabulated in the section property tables of Part 1 of the SCM for all rolled shapes. For other members Ag needs to be computed.
Example 3.1 shows how this limit state is applied. As you follow the example you will notice that the member is adequate for LRFD but not for ASD. You will want to read the observations in the example problem to find out why this is so.
Sample Spreadsheet Pn Computation
There are probably many ways to arrange this computation, but here is one. The shown spreadsheet both computes the "capacity" of the member (in terms of Ps,eq) and checks the capacity against the demand, or required strength, (Pu or Pa). Generally you will do either one or the other, not both. The values in the shaded cells are either entered manually or computed elsewhere and linked to these locations. Note that this spreadsheet only ANALYZES a given member. For design problems where the member size is unknown, you will need use a little algebra to solve the limit state equation for the required Ag then make decisions from there. In the end, however, you need to show that your final selection satisfies the limit state using some calculation similar to the one shown here.
| Tensile Yielding (SCM D2 & J4.1a) | Pn = AgFy | ||||||
| Ag | 2 | in2 | |||||
| Fy = | 50 | ksi | |||||
| Pn = | 100 | kips | |||||
| IF you need to determine capacity: | |||||||
| LRFD | ASD | ||||||
| ft = | 0.9 | Wt = | 1.67 | ||||
| ft Pn = | 90 | kips | Pn / Wt = | 60 | kips | ||
| CLF | 1.40 | CLF | 0.90 | ||||
| Ps,eq = | 64.3 | kips | Ps,eq = | 66.5 | kips | ||
| IF you need to check capacity: | |||||||
| LRFD | ASD | ||||||
| ft = | 0.9 | Wt = | 1.67 | ||||
| ft Pn = | 90 | kips | Pn / Wt = | 60 | kips | ||
| Pu | 50.00 | kips | Pa | 35.00 | kips | ||
| Pu/ftPn = | 55.6% | kips | Pa / (Pn / Wt ) = | 58.5% | kips | ||
| Okay | Okay | ||||||
<<< Previous Section <<< >>> Next Section >>>