|
|
|
|
|
|
|
|
|
|
|
Section 8.6.3
Transverse Stiffeners for Shear
Last Revised: 06/22/2023
|
Figure 8.6.3.1 |
|
|
As previously discussed, transverse stiffeners for shear (i.e., web stiffeners) are used to increase shear capacity in a beam web. This is accomplished by providing out of plane stiffness with transverse web stiffeners. Figure 8.6.3.1 shows transverse stiffeners (aka web stiffeners) in a bridge application.
SCM G2.1 and G2.2 are used to compute the shear strength of steel I-beam webs. The equations for shear capacity are, in part, a function of kv which is a factor that accounts for the presence of transverse stiffeners. Using the criteria of this section, a designer selects the spacing, a, of the stiffeners to develop the required shear strength in the beam. Note that close spacing results in higher shear capacity for non-compact and slender webs.
SCM G2.4 describes the criteria for the design of the actual stiffeners. The objective is to select the thickness, t, and width, b, of the stiffener plates.
Stiffener plates can be applied to either just one side of the web or both sides. In either case the stiffeners must provide sufficient moment of inertia to prevent out of plane buckling. Figures 8.6.3.2 and 8.6.3.3 show the dimensions associated with each case.
| Figure 8.6.3.2 Transverse Stiffeners on Both Sides |
|
|
|
Figure 8.6.3.3 |
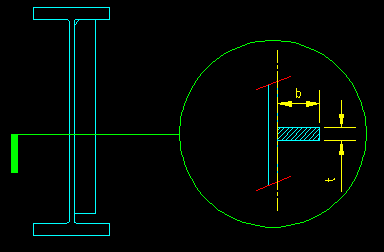 |
The stiffeners are typically steel plates welded to the web as shown in the figures. However, it is possible to bolt angles and other shapes to the web to accomplish the same purpose. In these cases, basic principles of statics are used to compute the moments of inertia for the attached elements.
The goal is to provide a stiffener plate with a moment of inertia greater than or equal to what is required. Mathematically the goal is expressed as:
Ist > Ireq'd = Ist2 + (Ist1-Ist2)rw
Determining the Required Moment of Inertia
The computation of the required Moment of Inertia in SCM 15th edition is a lot more complicated than in prior versions and has persisted into the SCM 16th edition.
The required moment of inertia to be provided by the transverse stiffener plates is given in SCM G2.4(e) as:
Ireq'd = Ist2 + (Ist1-Ist2)rw
The various terms are defined in SCM G2.4(e).
While SCM equation G2-18 is intimidating on first glance, computing Ist1 is fairly straight forward. Making a substitution for the rw term in SCM equation G2-18:
Ist1 = (h4*(max[Fyw/Fyst,1])1.3)*(Fyw/E)1.5/40
Ist2 will be smaller than Ist1 as it takes less Moment of Inertia to resist web shear buckling resistance than the full shear post buckling resistance of the web. SCM equation G2.4(e) essentially reduces the Ireq'd to levels below Ist1 for web shear buckling. Consequently, there is a user note in G2.4 that permits the designer to conservatively use Ist1 as the required Moment of Inertia.
Ist2 is computed using SCM equation G2-19 which can be written as:
Ist2 = max[(2.5/(a/h)2 - 2), 0.5]*bptw3
The value of computing Ist2 is questionable if performing these computations manually as it does little to reduce the required Ireq'd. It is possible to program the computation if developing an computer based beam/girder design tool.
Determining the Actual Moment of Inertia
SCM G2.4(e) states that the moment of inertias are computed about an axis at the center of the web for double stiffeners or at the face of the web for single stiffeners. This is done for plate stiffeners with the following equations:
Double stiffeners (see Figure 8.6.3.2 for dimension definitions):
Ist = t [ (2 b + tw)3 - tw3 ] / 12
Single stiffeners (see Figure 8.6.3.3 for dimension definitions):
Ist = t b3 / 3
Note that for stiffeners of different geometry than shown above, you will need to use basic principles of Statics to compute the moments of inertia required by SCM G2.4(e).
Stiffener Compactness Criteria
SCM G2.4(d) requires that the width/thickness ratio of the stiffener plates be below a point at which would cause local buckling of the plates. This limit will provides a relationship between plate width, b, and plate thickness, t, that will be used in the final selection of the stiffener plates.
Solving SCM equation G2-12 for t results in:
t > 1.79 b sqrt(Fyst/E)
Selecting Stiffener Plate Dimensions
As discussed above, the design objection is to pick stiffeners whose moments of inertia meet the following criteria:
Ist > Ireq'd
And for which the plate width/thickness ratio (b/t) is below a maximum value.
For plate stiffeners the search is for two variables, b and t. One easy approach is to select the desired b and solve for a required t.
For double stiffeners this results in:
t > MAX[12 Ireq'd / [ (2 b + tw)3 - tw3 ] , 1.79 b sqrt(Fw/E)]
For single stiffeners this results in:
t > MAX[3 Ireq'd / b3 , 1.79 b sqrt(Fw/E)]
Using these equations, different values of plate width, b, can be chosen used to solve for the associated values for plate thickness, t. The designer then picks the combination that best meets the demands of the project.
Length and Connection of Stiffeners
You should take the time to read the paragraph in SCM G2.4 that deals with the details associated with stiffener design. Note that it is common to stop the stiffeners short of the tension flange.
<<< Previous Section <<< >>> Next Section >>>

