|
|
|
|
|
|
|
|
|
|
|
Section 8.8.6
Example Problem 8.6
|
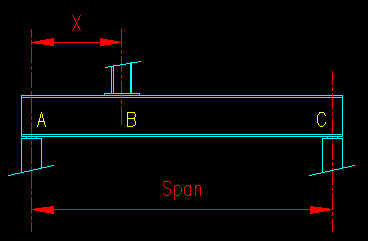
Figure 8.8.6.1 |
|
|
The example problems presented in this section have a spreadsheet solution. You will need this file to follow along with the presented solutions. You can click on the following link to get the file:
Chapter 8: Excel Spreadsheet Solutions
Given: A W18x35 is to be used as a transfer girder to transfer a column load over an opening as shown in Figure 8.8.6.1. The supporting wall is a 10 inch thick concrete wall with a 28-day compressive strength, f'c, of 3,000 psi. Use the preferred steel for all steel components.
Wanted: Design bearing plates for the following conditions:
- Size the bearing plate at point A for a reaction force equal to 75% of the shear capacity of the W18x35.
- Size the bearing plate at B for a load equal to 125% of the shear capacity of the W18x35. Assume that the supported column length along the beam is 8".
- Size the bearing plate at point B for a reaction force equal to 50% of the shear capacity of the W18x35.
As opposed to using a specified column load, we are, in this problem, designing for a percent of capacity. Note that the column load is larger than the shear capacity of the member. If you develop the shear diagram for any value of span and x, you will find that the column does not create a shear in the beam that is above its capacity.
In part (a) of the problem, the web length, lb, required to satisfy the web crippling limit state is longer than the supporting wall is wide. This means that bearing stiffeners are in order. While we are not designing the bearing stiffeners, we will say for now that they are to be added and make the N dimension of the plate equal to wall thickness.
Using the computation for the limit state of bearing on the concrete, we find the dimension B. In this case the bearing plate N takes up the full width of the wall, so the value of A2 equals A1 and there is no bonus for confinement of the compression area. There is a cell in this computation labeled "temp. #". This is the non-changing part of SCM equation J10-5 and is used as an intermediate step in setting up the spreadsheet formulas in the following cells.
The cantilevered part of the plate "beam", (B-k)/2, is relatively small for this plate, resulting in a fairly thin bearing plate.
For part (b) the dimension "N" of the plate in this part is dictated by required web crippling length, lb, of the supporting beam. This plate is relatively long. The use of bearing stiffeners could substantially reduce the need for this length. Regardless, we are not adding bearing stiffeners in this problem so will use the computed length.
Since the cantilever part, (N-0.95d)/2 in this case, is so long, we end up with a fairly thick plate for this bearing plate. (Again, the presence of bearing stiffeners would reduce this requirement as well.) The final plate thickness was chosen based on 1/4" plate thickness increments.
Finally, part (c) of the problem is very similar to part (a). The difference now is that the plate does not cover the full width of the wall. To take maximum advantage of the A2/A1 ratio in equation J8-2 we have elected to place the bearing plate in the middle of the wall. This maximizes A2 and results in a minimum value for B.
Also, in part (c) we chose to find a plate width B that results in a plate thickness that is the same as found on part (a). This is convenient so as to allow the beam to be level if the bearing surfaces of the plates are at the same elevation.
In summary, note that the plate width, B, is narrower than flange width of the supported beam in parts (a) and (c). It will be difficult to connect the beam to the bearing plate. It might be advantageous to make the plate wider than the beam flange as the connection is detailed. If the plate is made wider, the plate will also need to be made thicker to distribute the load evenly under the plate. The required thickness equation will indicate what thickness is to be used.
<<< Previous Section <<< >>> Next Section >>>