|
|
Section 3.6
Bolt Bearing on Holes
Last Revised: 07/08/2023
Later we will be discussing bolts in more detail than we will in this section, but there are a couple of concepts that we must introduce here as they affect member strength as opposed to bolt strength.
First, bolts are considered to transfer force between the connected members in one of two ways. One of the ways bolts transfer force is by what we call "bearing". The other means is by friction.
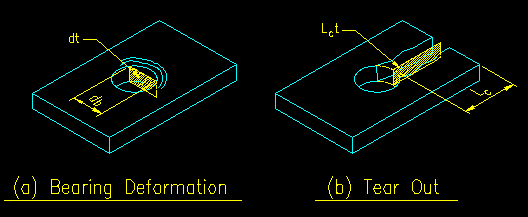
The bearing method assumes that the bolt contacts the side of a hole and that there is a compressive force between the bolt and the side of the hole. The magnitude of this compressive force is limited by the strength of the member's material to handle this compressive force. The provisions for this failure mode are found in SCM J3.11 (SCM page 16.1-143). According to the commentary on this section (SCM page 16.1-504) the strength is controlled by either bearing deformation or by tear out. Figure 3.6.1 illustrates the two modes of failure and the associated areas used in the limit state equations.
Figure 3.6.1
Bolt Hole Failure Modes
The Limit State:
The basic limit state follows the standard form. The statement of the limit states and the associated reduction factor and factor of safety are given here:
| LRFD | ASD |
| Pu < ftRn | Pa < Rn/Wt |
| Req'd Rn = Pu/ft < Rn | Req'd Rn = Pa Wt < Rn |
| Pu / (ftRn) < 1.00 | Pa / (Rn/Wt) < 1.00 |
| ft = 0.75 | Wt = 2.00 |
The values of Pu and Pa are the LRFD and ASD factored loads, respectively, applied to the member.
Nominal Bolt Bearing Strength, Rn:
The nominal resistance, Rn, of a single hole is the minimum value of the two limit states: tear out and bearing deformation. Equations J3-6 (SCM page 16.1-143) give values for several different hole types and service conditions. The total force that can be resisted is the lowest force per bolt times the number of bolts. It is worth noting that there is a basic assumption that all bolts are equally stressed at any given instant in time. We'll say more about this later, but the root of the assumption is that all bolts are equally deformed at any time and as a result they all carry the same force per bolt.
SCM J3.11(a) applies any time a bolt bears on the side of a hole where the bearing surface is curved. This is the case shown in Figure 3.6.1. This includes standard and oversized round holes as well as short slotted holes regardless of the direction of force. (Note that SCM Table J3.3 gives dimensions for the various hole definitions.) In these cases, the material surrounding the holes (particularly on each side) participates materially in carrying some of the bearing force. For long slotted holes with the direction of force parallel to the direction of the force you have a similar condition once the bolt meets the end of the slot.
Another decision that needs to be made when using SCM J3.11(a)(1)(a) or SCM J3.11(a)(1)(b) is whether or not deformation of the hole at service loads is a design consideration or not. In most cases deformation at service loads not an issue. In cases where loads reverse or added end rotation is an issue, then you might want to use the more restrictive values associated with SCM J3.11(a)(1)(a) and SCM J3.11(a)(1)(b).
You will notice that, like all the equations we've dealt with so far, equations J3-6 consist basically of a stress times an area to arrive at a force.
For the tear out limit state, the area equals the material thickness, t, times the clear distance in the direction of force of the tear out, Lc. The area in question is illustrated in Figure 3.6.1(b). Lc is the minimum such value on your member. The stress is some constant (1, 1.2, or 1.5 depending on which criteria you use) times Fu. Fu is used because this is a fracture/rupture situation.
The bearing deformation limit state is based on a maximum bearing stress (a constant times Fu) times the projected area of the contact surface normal to the direction of force. The area is shown in Figure 3.6.1(a) and equals the actual diameter of the bolt times the thickness of the plate.
Section J3.11(a)(2) gives the limit state equations for a long slotted hole loaded perpendicular to the long axis of the slot. In this case, there is less support from adjacent material so the nominal resistance is lower. This section also considers both bearing and tearout.
Sample Spreadsheet Computation
As always, there are probably many ways to arrange this computation, but here is one. The values in the shaded cells are either entered manually or computed elsewhere and linked to these locations. Note that this spreadsheet only ANALYZES a given member. For design problems where the member is unknown, you will need to solve the limit state equation for the required Lc, tpl, db, and/or nb then make decisions from there. In the end, however, you need to show that your final selection satisfies the limit state using some calculation similar to the one shown here.
| Bolt Bearing (J3.10) | ||||||||
| deformation at bolt hole IS a design consideration: Rn = min[1.2LctFu, 2.4dtFu] | ||||||||
| deformation at bolt hole IS NOT a design consideration: Rn = min[1.5LctFu, 3.0dtFu] | ||||||||
| long slotted holes perpendicular to force: Rn = min[1.0LctFu, 2.0dtFu] | ||||||||
| Deformation at the bolt hole is not a design consideration | ||||||||
| Use Equations J3-6b and J3-6d | ||||||||
| tpl = | 0.5 | in | End dist | 1.5 | in | |||
| db = | 0.75 | in | Lc = | 1.0625 | in | |||
| Fu = | 65 | ksi | num bolts | 12 | bolts/connection | |||
| Tear | Bearing | Use | Use | |||||
| Out | Deformation | |||||||
| (k/bolt) | (k/bolt) | (k/bolt) | (k) | |||||
| Fu factor | 1.5 | 3.0 | ||||||
| Rn | 51.8 | 73.1 | 51.8 | 621.6 | ||||
| Controlling Rn = | 621.6 | k | ||||||
| IF you need to determine capacity: | ||||||||
| LRFD | ASD | |||||||
| ft = | 0.75 | Wt = | 2 | |||||
| ft Pn = | 466 | kips | Pn / Wt = | 311 | kips | |||
| CLF | 1.40 | CLF | 0.90 | |||||
| Ps,eq = | 333.0 | kips | Ps,eq = | 345.3 | kips | |||
| IF you need to check capacity: | ||||||||
| LRFD | ASD | |||||||
| ft = | 0.75 | Wt = | 2 | |||||
| ft Pn = | 466 | kips | Pn / Wt = | 311 | kips | |||
| Pu | 50.00 | kips | Pa | 50.00 | kips | |||
| Pu/ftPn = | 10.7% | Pa / (Pn / Wt ) = | 16.1% | |||||
| Okay | Okay | |||||||