|
References |
|
|
Section 3.6.4
Example Problem 3.4
Last Revised: 04/08/2018
Reference Files:
3.6.4 Example Problem 3.4|
|
|
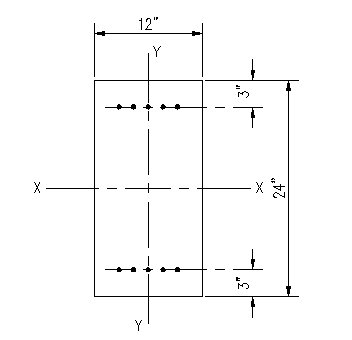
Figure 3.6.4.1 |
Given: The section shown is Figure 3.6.4.1 is made from concrete with f'c = 3,000 psi. The reinforcing steel consists of 5 bars made from ASTM A615 Gr. 60 rebar.
Wanted: Compute the nominal pure bending moment capacity for the given beam section for the following rebar sizes:
- #5
- #8
- #10
Solution:
This is the same problem as Example Problem 3.3 with the addition of steel near the compression face.
For this problem we can determine the location of the neutral axis, c, directly using axial force equilibrium.
Pn = 0 = Cc + Ts1 + Ts2
There are at least eight permutations of this equation to consider:
- Both groups of steel yield and the top steel (Ts1) falls within the Whitney Stress Block.
- Both groups of steel yield and Ts1 does not fall within the Whitney Stress Block.
- Neither group of steel yields and Ts1 falls within the Whitney Stress Block.
- Neither group of steel yields and Ts1 does not fall within the Whitney Stress Block.
- Ts1 yields but the steel at the bottom (Ts2) does, and Ts1 falls within the Whitney Stress Block.
- Ts1 yields but Ts2 does, and Ts1 does not fall within the Whitney Stress Block.
- Ts1 does not yield but Ts2 does, and Ts1 falls within the Whitney Stress Block.
- Ts1 does not yield but Ts2 does, and Ts1 does not fall within the Whitney Stress Block.
Case (a)
In example 3.3, the same beam (using #5 rebar) without compression steel has a lower limit on the compression block, a, of 3.04". The addition of compression steel should cause this number to get smaller, so it will be assumed that Ts1 does not fall within the Whitney Stress Block. Ts1 is also likely to close to the neutral axis at location c, so it will be assumed that Ts1 does not yield. Since Ts2 yielded in example 3.3 and c is likely to get shorter, then assume that Ts2 yields. This means that our best bet is to start with permutation 8. We will need to verify our three assumptions when we are done.
For example, permutation #4 will be considered first. For this permutation, the axial force equilibrium equation is written as:
0 = -0.85f'cbb1c + As1Es[(c-d1)(-0.003/c)] + As2fy
0 = 0.85f'cbb1c2 - (As2fy -0.003As1Es)c - 0.003As1Esd1
0 =26.01c2 + 41.85c - 404.55
Solving the quadratic equations yield c = 3.22 in. Now we need to check our assumptions:
Assumption 1: Ts1 does not yield.
The strain in Ts1 = -.003*(3.22 in - 3 in)/(3.22 in) = -.00021. The yield strain for the specified bars is fy/Es = .00207. Since the absolute value of the strain in Ts1 (0.00021) is less than the yield strain, the assumption is valid.
Assumption 2: Ts2 yields.
From example problem 3.3, cb = 12.4". Since c < cb, the assumption that Ts1 yields is true.
Assumption 3: Ts1 does not fall within the Whitney compression block.
The depth of the Whitney Stress Block, a, is b1c = 2.74 in. Since a < d1 (3 in), the assumption is valid.
Since all our assumptions are valid, we chose the one correct equation out of the eight possible permutations. If any one of the assumptions had been invalid, the assumptions must be changed and additional equations would need to be investigated until one is found to satisfy all assumptions.
It should be noted that correctly solving these equations is difficult as they open to many algebraic errors. In preparing the solution for this example, for example, the problem had to be reworked several times before all the errors were found and corrected. This took quite a bit of time.
The alternate to this approach is to develop a spreadsheet implementing equation Equation 3.5.7. The spreadsheet accompanying this example does that. The spreadsheet looks like:
| Strong Axis Bending | ||||||||
| c = | 3.22053 | in | a = | 2.74 | in., measured from compression face | |||
| Concrete Area and Centroid Computations | ||||||||
| Width | Height | Area | Ycf | Ycf*A | ||||
| (in) | (in) | (in2) | (in) | (in3) | ||||
| Acg | 12 | 2.74 | 32.85 | 1.37 | 44.96 | |||
| As1 | 0 | 3 | 0 | |||||
| As2 | 0 | 21 | 0 | |||||
| Total | 32.85 | 44.96 | ||||||
| Ac = | 32.85 | in^2 | ||||||
| Ycf = | 1.37 | in (center of area measured from the compression face) | ||||||
| Y = | 16.63 | in (Y location of center of area measured from centroidal X axis) | ||||||
| X = | 0.00 | in (X location of center of area measured from centroidal Y axis) | ||||||
| Area | Ycf | strain | stress | Force | ||||
| (in^2) | (in) | (ksi) | (k) | |||||
| Conc | 32.85 | 1.37 | ---- | -2.55 | -83.77 | |||
| Bar 1 | 1.55 | 3 | -0.00021 | -6.0 | -9.23 | |||
| Bar 2 | 1.55 | 21 | 0.016562 | 60.0 | 93.00 | |||
| Pn = | 0.0 | |||||||
To find the case of pure bending, the value of c is varied until Pn = 0. In Microsoft Excell, the "goal seek" function can be used to do this. It actually took less time to program and debug the spreadsheet than it did to solve the equilibrium equation by hand. Plus, once programmed and debugged, the spreadsheet can be used in the future for similar problems.
Now that we have the location of the internal forces and their magnitudes, we can solve for the nominal moment capacity, Mnx.
Taking moments about the centroidal X-X axis, we get
Mnx = (83.77 kips)*(24"/2 - 1.37") + (9.23 kips)*(24"/2 - 3") + (93.00 kips)*(21" - 24"/2) = 1,811 in-k
Mnx = 151 ft-k <--- Answer
Now, let's compare this to Mnx for the singly reinforced version of this beam.
In both cases the result for Mnx is the same when the answer is expressed in three significant figures. If the answer is taken to five significant figures:
Mnx = 150.97 ft-k for the singly reinforced beam while Mnx = 150.89 ft-k for the doubly reinforced beam. The result is a slight DECREASE in moment capacity with the addition of the reinforcing steel. This is a rare case where the compression steel fall slightly below the concrete compression block, causing a slight decline in the distance between the resultant forces of the internal couple.
The bottom line is that the addition of compression steel did not increase the bending strength of the beam, in this case.
Solution Summary
Parts (b) and (c) of this problem were solved using the spreadsheet provided with this problem. Table 3.6.4.1 summarizes the findings and compares the results with the singly reinforced beams.
|
Table 3.6.4.1 Example Problem 3.4 Solution Summary |
||||||
| Case | Rebar Size | Singly Reinforced | Doubly Reinforced | Strength Increase | ||
| Mnx (ft-k) | c (in) | Mnx (ft-k) | c (in) | |||
| a | #5 | 151 | 3.58 | 151 | 3.22 | 0.00% |
| b | #8 | 338 | 9.11 | 336 | 4.71 | -0.59% |
| c | #10 | 436 | 13.02 | 579 | 5.53 | 32.80% |
There are a few things to note about the solution.
- In case (c) the beam, without the addition of compression steel, now meets ACI 318 ductility requirements, however it is likely to have significant deflection issues for reasons explained in the beam design chapter. The great increase in strength is due to the fact that the addition of the massive compression steel raised the neutral axis to the point that c < cb, thus causing the tension steel to yield. So, in addition to increasing the distance between the forces in the internal couple, the magnitude of the forces was increased as well. This is an extreme and unusual situation.
- Cases (a) and (b) are more common conditions. In both of these cases, doubling the steel in the beam by adding it to the compression side did not increase the strength at all. It would have been more effective to place the additional steel with the tension steel.
- Adding steel to the compression zone decreases c, increasing the strain in the tension steel. This adds to the ductility of the member.