Interaction Diagrams

Up to this point, only the strengths associated with a randomly selected neutral axis have been discussed. Little mention has been made of computing the strengths related to a particular set of applied forces. That problem will be solved in this section.

Typically, design starts with a known value of internal forces (axial force, moments, and shears) resulting from a structural analysis. The goal is to find a member which has sufficient strength to support these forces. For now, we are concentrating on axial force and moments, which cause normal stress on a cross section. Shear will come in another chapter.

Quite frequently, linear members (i.e. beams and columns) have special cases of the possible three possible normal internal forces, (P_u, M_ux, and M_uy). For example, the most common special cases are:

For any other case we need to determine the location and orientation of the neutral axis such that we can show that the strengths exceed the applied forces. Interaction curves/surfaces can help us do this.

As the location of the neutral axis, c, is varied, different strengths, P_n, M_nx, and M_ny are found. Each of the conditions represents an internal force combination which is at the limit of the member strength. If the member is symmetrical (both in shape and reinforcing) about the centroidal axis perpendicular to the neutral axis (a very common condition) then we can make a two dimensional interaction curve. The interaction curve represents all the possible failure combinations for the member when bent around the axis which is perpendicular to the axis of symmetry. Figure 3.4.1 shows the section used in Example Problem #1. In this case, we are considering bending about the X-X axis. You will want to take a close look at this problem.

A spreadsheet has been developed to solve this problem for any location, c, of the neutral axis (the neutral axis being parallel to axis X-X). Using the spreadsheet, enough values of P_n and M_nx were determined (Table 3.4.1) to plot a curve (Figure 3.4.2).

Note that the computations used tension positive notations however most published interaction diagrams are for sections used primarily as compression members (columns) so compression is positive. For graphing purposes only, the negative compression values are plotted on the positive side of the scale.

Table 3.4.1
Interaction Data

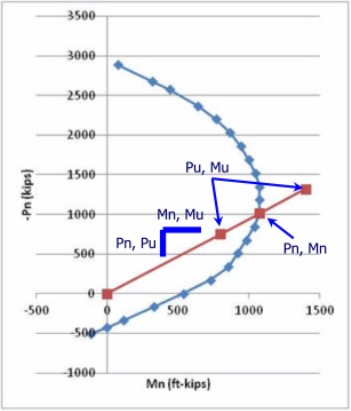
Figure 3.4.2
Example Problem #1 Interaction Diagram

Interaction Diagram Information
C	P_n	M_nx
(in)	(k)	(ft-k)
0.001	505	-113
1.8	426	0
2.18	335	116
3.31	166	330
5.24	0	538
8.12	-170	728
11.28	-339	857
13.64	-508	922
15.82	-677	984
17.53	-846	1038
19.3	-1015	1077
20.91	-1184	1074
22.53	-1353	1075
24.21	-1522	1045
25.93	-1691	1001
27.7	-1861	942
29.5	-2031	867
32.4	-2201	768
35.8	-2371	640
40	-2573	443
42.5	-2677	321
107	-2890	75

The section shown in this example is most likely to be used as a single axis of bending beam. Consequently, it has only one axis of symmetry. As a result of the lack of symmetry about the X-X axis, the cases for c = 0 and c= very large, have moment associated with them. In a doubly symmetrical member M_nx would equal zero for these two cases.

The other special case of interest is pure bending, which occurs when P_n = 0. In this case, c = 5.24" and M_nx = 538 ft-kips. This is the theoretical maximum moment that can be applied in the absence of axial force and the basis for determining the bending capacity of a member acting only as a beam.

However, you will also notice that the maximum computed M_nx for this member is 1,077 ft-k. To be able to utilize this moment capacity an axial force of 1,015 k must be applied simultaneously.

In reality, members have three dimensional interaction diagrams since it is possible that the structural analysis will yield P_u, M_ux, and M_uy combinations. This situation is very common in column design. Depending on the location and orientation of the neutral axis, as well as any lack of symmetry in cross section or rebar layout, strength analysis will yield non-zero values for P_n, M_nx, and M_ny for a given situation. Each unique combination of P_n, M_nx, and M_ny can be plotted in three dimensional space. With enough computational effort enough points can be computed to generate a "failure" surface. Each point on the surface represents a strength limit for a given position and orientation of neutral axis. Figure 3.4.2 shows representative 3D interaction diagram for a rectangular column. The blue axes in the horizontal plane are the principle axes (X and Y) for the section. The values of M_nx and M_ny are plotted relative to these axis. The vertical axis is used to plot the axial capacity, P_n, values. Generation of these surfaces can only be reasonably done by a computer.

Similar to the 2D interaction diagrams, plotted points of P_u, M_ux, and M_uy (resulting from a structural analysis) that fall within the surface will not result in member failure. Points that plot out side the surface exceed the nominal strength of the member and would result in member failure before attainment of the load combination.

The 2D interaction curves and 3D interaction surfaces denote (P_n, M_nx, M_ny) combinations causing compressive concrete failure for an infinite number of neutral axis locations and orientations. Any actual (P_u, M_ux, M_uy) combinations that fall within the curves/surfaces will, theoretically, not cause failure of the member. As we will see in later sections, modifiers are applied to the (P_n, M_nx, M_ny) combinations to account for variation in test results and safety.

Note that the red line in Figure 3.4.2 starts at the origin and passes through a point on the interaction curve. The slope of this line is P_n/M_n. Any applied force combination (P_u, M_u) having the same proportional relationship (P_u/M_u) falls on the same slope line. The only way to numerically ensure that an applied load is within the capacity of the member is to determine the (P_n, M_n) combination with the same relationship and show that either P_n > P_u or M_n > M_u. In Figure 3.4.2 two P_u, M_u combinations have been plotted along the slope line. One is within the curve (theoretically acceptable) and one outside the curve (theoretically unacceptable).

In order to check adequacy against a particular (P_u, M_ux, M_ny) combination, it is necessary to find the (P_n, M_nx, M_ny) combination that is on the same line radiating from the center of a coordinate system. This means that the following conditions must be met:

Once these conditions are met, then any of the following will, theoretically, be ensure adequacy:

In actuality, the nominal strength values will be reduced by modifiers, as will be shown in later chapters.

For 2D situations, the equations with terms related to the axis of symmetry can be ignored.

This condition ensures that there is sufficient strength available to support the applied forces.

As most members are subjected to many loading cases, it is sometime convenient to compute and plot the interaction diagram then simply plot all the P_u, M_u combinations on the diagram. If all the combinations are within the curve, appropriately modified as shown in later chapters, then the member is theoretically capable of supporting the various loading scenarios.