|
References |
|
|
Section 3.6.3
Example Problem 3.3
Last Revised: 04/08/2018
Reference Files:
3.6.3 Example Problem 3.3|
|
|
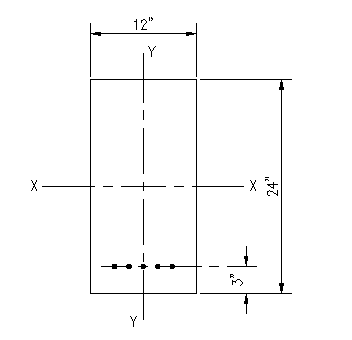
Figure 3.6.3.1 |
Given: The section shown is Figure 3.6.3.1 is made from concrete with f'c = 3,000 psi. The reinforcing steel consists of 5 bars made from ASTM A615 Gr. 60 rebar.
Wanted: Compute the nominal pure bending moment capacity for the given beam section for the following rebar sizes:
- #5
- #8
- #10
Solution:
For this problem we can determine the location of the neutral axis, c, directly using axial force equilibrium.
Pn = 0 = Cc + Ts
There are only two internal forces acting on the section: The tension in steel and the compression in the concrete. An assumption must be made concerning the stress in the steel.
If c < cb, then the steel has yielded and the steel stress equals fy.
If c > cb then the steel has not yielded and the steel stress equals the actual strain times the steel Modulus of Elasticity.
In order to use the axial equilibrium equation directly, we need to made an assumption regarding the state of the steel stress so that the equation can be written and solved. The assumption will need to be verified.
For now, we will assume that the steel yields.
The concrete area equals the concrete stress, 0.85f'c, times to area of concrete bounded by the physical boundaries of the section and the line a. For the rectangular section with no reinforcing steel in compression area, Ac = ba.
The resulting equilibrium equation is:
0 = -0.85f'cba + Asfy
Solving for a, we get:
a = Asfy/(0.85f'cb)
To find c, we divide a by b1.
c = a/b1 = Asfy/(0.85f'cbb1)
For case (a):
b1 = 0.85 (see ACI 318-14 22.2.2.4.3)
a = (5 bars)(0.31 in2/bar)(60 ksi)/[0.85(3 ksi)(12 in)] = 3.04"
c = 3.04"/0.85 = 3.58"
We can now check our assumption that the steel yielded by comparing c to cb. We compute cb using Equation 3.5.1, where dmax is the distance from the compression face to the center of the steel group for this problem. Note that cb is the same for all cases in this problem since it dependent only on the location of the tension steel, not the area of steel.
cb = .003(24"-3")/(.003+(60 ksi)/(29,000 ksi)) = 12.4 in > 3.58" ... Assumption valid for case (a)
The nominal strong axis bending moment, Mnx, can now be computed. We can use Equation 3.5.3 since we know that the steel yields for this case:
Mnx = (5 bars)(0.31 in2/bar)(60 ksi)(21" - 3.04"/2) = 1810 in-k
Mnx = 151 ft-k <--- Answer, case (a)
Note that ft-k are the preferable units.
Also note that we are not investigating Mny for this problem. This is because the resultant concrete and tension forces will be centered on the vertical centroidal axis and, as a result, do not cause moment about the Y-Y centroidal axis. So, by observation, Mny = 0.
For case (b):
a = (5 bars)(0.79 in2/bar)(60 ksi)/[0.85(3 ksi)(12 in)] = 7.75"
c = 7.75"/0.85 = 9.11" < cb = 12.4 in ... the assumption of steel yielding is valid
Mnx = (5 bars)(0.79 in2/bar)(60 ksi)(21" - 3.04"/2) = 4059 in-k
Mnx = 338 ft-k <--- Answer, case (b)
For case (c):
a = (5 bars)(1.27 in2/bar)(60 ksi)/[0.85(3 ksi)(12 in)] = 12.45"
c = 12.45"/0.85 = 14.65" > cb = 12.4 in ... the assumption of steel yielding is NOT valid
We have to back up now and assume that the steel does not yield. We go back to the equilibrium equation and replace the steel force term. This was done in section 3.5 and resulted in equation 3.5.4:
0 = 0.85(3 ksi)(12 in)(.85)c2 + 0.003(29,000 ksi)(5 bars)(1.27 in2/bar)c - 0.003(29,000 ksi)(5 bars)(1.27 in2/bar)(21 in)
0 = 26.01c2 + 552.45c - 11,601
c = 13.02 in > cb ... assumption valid: steel does not yield
The nominal moment, Mnx, can now be computed for the situation where the steel does not yield (equation 3.5.6):
Mnx = AsEs(0.003d/c - .003)(d
- a/2)
Mnx = (6.35 in2)(21 in)(29,000 ksi)[(13.02 in - 21 in)(-0.003/13.02
in)][(21 in) - 0.85(13.02 in)/2]
Mnx = (6.35 in2)(53.3 ksi)[(21 in) - (11.1 in)/2]
Mnx = 5,238 in-k
Mnx = 436 ft-k <-- Answer, case (c)
Solution Summary
This problem demonstrates the effect on Mn of increasing the amount of tension steel in a singly reinforced rectangular beam. As expected, the value of Mn increases with steel. It is also noted that the area in compression increases to match the increased force from the steel.
Case (c) illustrates the need to verify our assumptions regarding the yielding of the tension steel. When the stress in the tension steel is less than fy then the nominal moment capacity is reduced.
It should be noted that it will be shown in a later chapter that the beam in case (c) violates ACI 318 ductility requirements, so could not be used.