A Beginner's Guide to the Steel Construction Manual, 16th ed.

Chapter 6 - Buckling Concepts

© 2006, 2008, 2011, 2017, 2023 T. Bartlett Quimby

Buckling Basics

General Buckling

Local Buckling

Stability Analysis Methods

Example Problems

Homework Problems

References

Report Errors or Make Suggestions

Purchase Hard Copy

Make Donation

 

Section 6.5.3b

Example Problem 6.3

Grid 2 Columns

Last Revised: 06/24/2023

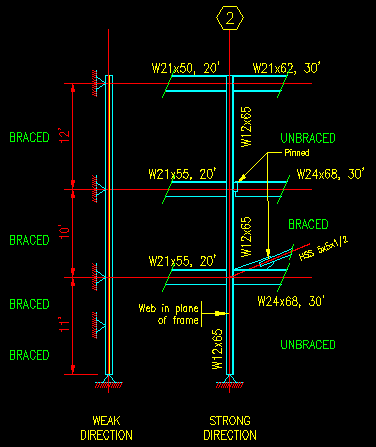
Figure 6.5.3.3 shows the support conditions for this column. We will start from the top and work our way down for computing the effective lengths. Note that, in the case of the grid 2 column that the weak direction is out of the plane of the frame.  This is different than what was used for the column on grid 1.

Figure 6.5.3.3
Grid 2 Column Diagrams

Third Floor Column Segment

Weak Direction: At this level and direction, there are no beams fixed to the column to create joint rotational restraint and the column is part of a frame that inhibits sidesway (i.e., it is braced) as stated on the drawings.

For these conditions, K = 1.00. This gives an effective length,

(KL)Y,23 = 1.0*12' = 12 ft.

The subscript used denotes the weak direction, "Y", on grid "2" on the third floor, "3".

Strong Direction: At this level, the support conditions are:

  • Sidesway is uninhibited. In the frame profile there are no braces on the third floor level so all the columns in this level are unbraced.
  • At the top of the column segment, W21x50 and W21x62 girders and the W12x65 column resist joint translation in plane. Note that joint rotation in the plane of the frame, in this case, causes bending about the strong axis of the girder and bending about the strong axis of the column. So we use Ix for the girder term and Ix for the column term:

    G2R = S(Ic/Lc) / S(Ig/Lg)
    G2R = [(533 in4)/(12 ft)] / [(984 in4)/(20 ft)+(1330 in4)(30 ft)]
    G2R = 0.475

    The subscript used is "2" for the grid line and "R" for the roof level. Note that "G" term need only be computed once for a joint. Joints are often shared by two column segments.

    Also note that we did not change the units so that they are all feet or inches. All the I terms are in4 and the L units are feet. Even without the unit conversion, all the units cancel, so save yourself the extra computational step! Check it out.
     

  • At the bottom of the column segment, a W21x55 girder and the W12x65 column resist joint rotation in plane. A W24x68 girder also frames into this joint, however it is pin connected and does not contribute to the in plane rotational restraint so it is ignored in the calculation. In this case the column is both above and below the joint, though it is of different lengths in each case. Note that joint rotation in the plane of the frame, in this case, causes bending about the strong axis of the girder and bending about the strong axis of the column. So we use Ix for the girder term and Ix for the column term:

    G23 = S(Ic/Lc) / S(Ig/Lg)
    G23 = [(533 in4)/(12 ft)+(533 in4)/(10 ft)] / [(1140 in4)/(20 ft)]
    G23 = 1.714

Entering the sidesway uninhibited nomograph on SCM page 16.1-651 with these two values and I get something close to 1.30. It is difficult to get a precise value from the nomographs so your value may be slightly different.

The effective length, then, for the 3rd floor column segment is:

(KL)X,23 = (1.30)(12 ft) = 15.6 ft

Second Floor Column Segment

Weak Direction: At this level and direction, there are no beams fixed to the column to create rotational restraint and the column is part of a frame that inhibits sidesway (i.e., it is braced) as stated on the drawings.

For these conditions, K = 1.00. This gives an effective length,

(KL)Y,22 = 1.0*10' = 10 ft.

Strong Direction: At this level, the support conditions are:

  • Sidesway is inhibited by a brace that prevents the second floor from moving laterally with respect the second floor. The brace is located between grids 2 and 3.
  • At the top of the column segment, a W21x55 girder and the W12x65 column resist joint rotation in plane. The W24x68 girder is connected to the column by a pinned connection and does not provide rotational restraint for the joint. Note that joint rotation in the plane of the frame, as discussed above, causes bending about the strong axis of the girder and bending about the strong axis of the column. So we use Ix for the girder term and Ix for the column term. We already computed this "G" term when determining the effective length of the third floor column segment so:

    G23 = 1.714
     

  • At the bottom of the column segment, W21x55 and W24x68 girders and the W12x65 column resist joint translation in plane. In this case the column is both above and below the joint, though it is of different lengths in each case. Note that joint rotation in the plane of the frame, in this case, causes bending about the strong axis of the girder and bending about the strong axis of the column. So we use Ix for the girder term and Ix for the column term:

    G22 = S(Ic/Lc) / S(Ig/Lg)
    G22 = [(533 in4)/(10 ft)+(533 in4)/(11 ft)] / [(1140 in4)/(20 ft)+(1830 in4)(30 ft)]
    G22 = 0.862

Entering the sidesway inhibited nomograph on SCM page 16.1-651 with these two values and I get something close to 0.800. It is difficult to get a precise value from the nomographs so your value may be slightly different.

The effective length, then, for the 2nd floor column segment is:

(KL)X,22 = (0.800)(10 ft) = 7.00 ft

First Floor Column Segment

Weak Direction: At this level and direction, there are no beams fixed to the column to create rotational restraint and the column is part of a frame that inhibits sidesway (i.e., it is braced) as stated on the drawings. Also, the column at this level, and in this direction, is braced at mid-height, as stated on the drawing.

For these conditions, K = 1.00. This gives an effective length,

(KL)Y,21 = 1.0*5.50' = 5.50 ft.

Strong Direction: At this level, the support conditions are:

  • Sidesway is uninhibited. In the frame profile there are no braces on the third floor level so all the columns in this level are unbraced.
  • At the top of the column segment, W21x55 and W24x68 girders and the W12x65 column resist joint rotation in plane. Note that joint rotation in the plane of the frame, as discussed above, causes bending about the strong axis of the girder and bending about the strong axis of the column. So we use Ix for the girder term and Ix for the column term. We already computed this "G" term when determining the effective length of the second floor column segment so:

    G22 = 0.862
     

  • At the bottom of the column segment, the base is pinned to the foundation. We will assume that the pinned connection is properly designed so that we can use the G specified on SCM page 16.1-652, in the paragraph labeled Adjustments for Columns with Differing End Conditions:

    G21 = 10.00

Entering the sidesway uninhibited nomograph on SCM page 16.1-651 with these two values and I get something close to 1.87. It is difficult to get a precise value from the nomographs so your value may be slightly different.

The effective length, then, for the 1st floor column segment is:

(KL)X,21 = (1.87)(11 ft) = 20.57 ft

Column Line Summary

Table 6.5.3.3 summarizes the resulting effective lengths for the column segments on grid 2.

Table 6.5.3.3
Grid 2 Results Summary
Weak Direction
Level (KL)Y
3 12 ft
2 10 ft
1b 5.5 ft
1a 5.5ft
 
Strong Direction
Level (KL)X
3 15.60 ft
2 8.00 ft
1 20.57 ft

<<< Previous Section <<<        >>> Next Section >>>