|
|
Section 6.5.1
Example Problem 6.1
Last Revised: 05/29/2023
The example problems presented in this section have a spreadsheet solution. You will need this file to follow along with the presented solutions. You can click on the following link to get the file:
Chapter 6: Excel Spreadsheet Solutions
In addition to the spreadsheet solution this problem also has a downloadable hand solution: BGSCMExample6_1.pdf
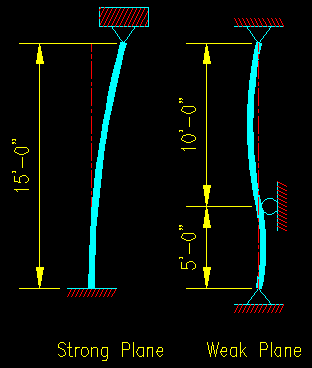
Given: A column is to be 15 ft long. In the strong plane, the column is part of an unbraced frame, one end is to be considered fixed and the other pinned. In the weak plane, the column is part of a braced frame, both ends are to be considered pinned and there is a lateral support provided 5 ft from one end.
Wanted: Determine the controlling effective length, KL, for the column using the following cross-sections. Note that the sections chosen are all approximately the same weight.
a) C 10x30; b) W 14x30; c) HSS 7x4x1/2; d) HSS 10x0.312
Solution:
|
Figure 6.5.1.1 |
Figure 6.5.1.1 illustrates the column conditions provided in the problem statement. These drawings help to demonstrate the accurate determination of effective lengths in each plane.
Effective Lengths
For this problem it is possible to determine the effective length coefficients from SCM Table C-A-7.1 on SCM page 16.1-511.
Strong Plane/Direction
In the strong direction there is only one length to consider (i.e., L = 15 ft).
The suggested effective length coefficient for this condition is 2.1, resulting in an effective length in the strong plane, (KL)x, of 31.5 ft.
Weak Plane/Direction
In this direction there are two lengths to consider. The lower five feet and the upper ten feet.
It is possible to create support conditions for which each of the two lengths has different effective length coefficients, but that is not the case here. Both are Euler columns with K = 1.0.
The result is that the upper ten feet provide the longest (and, hence, the controlling) length for the weak direction. The controlling (KL)y is 10 ft.
Member Slenderness
With the effective lengths determined, we can now compute the slenderness ratios in each plane for each of the given members. The plane with the largest slenderness ratio will be the controlling slenderness ratio for the column. Table 6.5.1.1 summarizes the results.
Table 6.5.1.1
Results Summary
| Controlling | |||
| Section | (KL/r) | Direction | |
| C10X30 | 179.6 | Weak | |
| W14X30 | 80.5 | Weak | |
| HSS7X4X1/2 | 157.5 | Strong | |
| HSS10X0.312 | 110.2 | N/A | |
The HSS 10x0.312 is a round section without any planes that can be considered "strong" or "weak", so for this member only the longest KL is needed for the computation.
Notice that the W14x30 is the least slender of the sections. It will, as a result, have the largest axial capacity of the group (as will be seen in the next chapter). The C10x30 will have the least axial compressive capacity of the group as the result of its large slenderness ratio.
It should be apparent that it is not always possible to determine the controlling direction for slenderness without doing the actual computations.