|
|
Section 10.5
Shear Anchor Design
Last Revised: 11/04/2014
SCM I3.2d specifies the shear force, V', that either can be, or is to be, transferred between the concrete and steel. This shear force is transferred between the beam and slab over a length from the location of maximum moment (where the internal forces are the greatest) and point of zero moment. Figure 10.5.1 illustrates the force on a free body diagram of a portion of a beam located between the zero moment location and the maximum positive moment.
Figure 10.5.1
FBD of a Partial Beam
Click on hotlinks in the image for larger
views
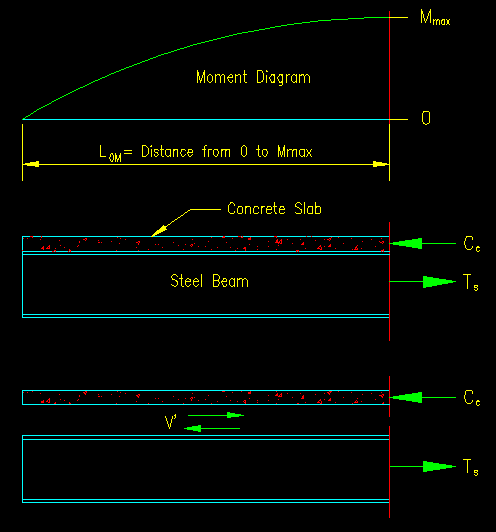
By statics, V' equals Cc and/or Ts. When the plastic neutral axis is in the steel beam, Cc is at its maximum value (Cc = .85f'cAc) since Ac is at its maximum value. When the plastic neutral axis is in the slab, Ts is at its maximum value (Ts = AgFy) since the entire section is in tension. Since Cc always equals Ts when the plastic neutral axis is in the slab and is at its maximum when the plastic neutral axis is located in the beam, the maximum value of V' will be the lesser of the maximum values of Cc or Ts. The smaller value controls.
Note that a free body of the other part of the beam to the right of the maximum moment would show that V' must also be developed on that side of the maximum moment as well.
For a section to be "fully composite" the shear anchors must provide strength that equals or exceeds the maximum V' resulting from concrete crushing (Ccmax) or tensile yielding (Tsmax) as discussed above. If the shear strength provided by the shear anchors (V' = sum of the strength of the shear anchors located between the location of maximum and zero moments) is less than what can be developed by concrete crushing or tensile yielding then the section is said to be "partially composite" and it's strength must be determined by the limit imposed by the shear anchor strength.
Design of Shear Anchors for Fully Composite Strength
When designing the shear anchors the total shear strength provided between zero and maximum positive moment locations is the sum of the shear strengths of all the shear anchors in that region. This value is mathematically expressed in SCM equation I3-1c.
V' = S Qn
The computation of the shear strength of a single anchor is addressed in SCM I3.2d(3) for studs and SCM I3.2d(4) for channel shear anchors.
Steel Headed Stud Shear Anchors, SCM I8.2a
Figure 10.2.1 has a series of images of typical steel headed stud anchors on a steel beam. The capacity of a stud to transfer shear is limited either by the shear strength of the stud or the strength of the concrete in contact with and surrounding the stud. SCM Equation I8-1 reflects these two limits. The equation can be written as:
Qn = minimum( 0.5 Asa sqrt(f'c Ec), RgRpAscFu)
The definitions of the variables are given in SCM I8.2a. You should review these terms. A commonly used value of Fu for available studs is 65 ksi. This value is to be verified with the supplier of the studs during the design process.
SCM Table 3-21 (SCM pg 3-209) lists Qn values of commonly used studs and concrete strengths.
Steel Channel Anchors
Steel channel anchors are small channel sections welded to the top flange of the beam. The channels are arranged so that they are transverse to the beam axis. These shear anchors are not typically used in conjunction with steel decking. The equation for the nominal strength of a channel shear anchor involves terms from the steel and the concrete. SCM equation I8-2 is used to compute the strength of a steel channel anchor.
Required Number of Anchors
For full composite action, the number of shear anchors is determined by writing a design inequality where the strength provided the shear anchors equals or exceeds that maximum V' provided by the steel or concrete.
(num. anchors)*Qn > min(Ccmax, Tsmax)
num. anchors > min(Ccmax, Tsmax)/Qn
This computation provides us with the number of anchors required between the location of zero and maximum moment (SCM I8.2c). This is HALF the total number of anchors required since the same number is required on the other side of the moment diagram.
Size and Spacing of Anchors
SCM I8.2d requires that the anchors be spaced uniformly along the flange between the locations of zero and maximum moment.
There are also some other limits that must be met for shear stud anchors:
- The diameter of the stud, dsc, cannot exceed 2.5 times the thickness of the beam flange (dsc < 2.5 tf, see SCM I8.1).
- There must be at least 1" of lateral concrete cover. This means that the clear distance between studs must be at least 1". The smallest center-to-center distance equals 1" plus the diameter of the head of the stud.
- The distance from the center of the anchor to the nearest free edge of concrete must be at least 8" for normal weight concrete or 10" for lightweight concrete.
- The longitudinal center-to-center stud spacing along the beam axis must be greater than or equal to 6 dsc, except within ribs of steel decking, the spacing must be greater than or equal to 4 dsc.
- The transverse center-to-center stud spacing on the beam flange must be greater than or equal to 4 dsc.
- The maximum center-to-center spacing of studs < min( 8*slab thickness, 36 in).
<<< Previous Section <<< >>> Next Section >>>