| Overview |
| Equivalent Stiffness |
| Transformed Moment of Interia, ITR |
| Example Problems |
| Homework Problems |
| Report Errors or Make Suggestions |
Section ITR.4
Example Problem ITR01
Composite Steel/Concrete Beam
Last Revised: 11/20/2007
Figure ITR01.1 shows a steel beam with a concrete slab attached to the top flange and a steel cover plate attached to the bottom flange. The goal of this problem is to compute the major axis transformed moment of inertia for the beam.
Figure ITR01.1
Composite Steel/Concrete Beam
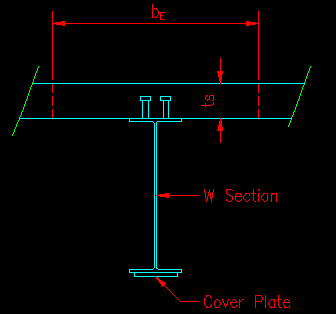
Given: bE = 63 in, ts = 4", W18x35 steel beam, 1/2"x4" steel cover plate, normal weight concrete with a 28-day strength (f'c) = 3 ksi.
Wanted: The transformed moment of inertia, Ixtr.
Solution: Transform the concrete into equivalent steel.
To do this you need to find Ec so that you can compute n. According to ACI 318, Ec is found by:
Ec = 33 w1.5 sqrt(f'c) = 33 (145 pcf)1.5 sqrt(3,000 psi)
Ec = 3.156x106 psi
Now we compute n:
n = 29 / 3.156 ~ 9.0
To transform the section into all steel, we need to divide the concrete dimension parallel to the axis (i.e. bE) by n and draw the new section.
bE / n = 63" / 9 = 7.00"
The transformed section is shown in Figure ITR01.2
Figure ITR01.2
Transformed Section

The following computation computes the location of the Elastic Neutral Axis (ENA) relative to the top of the slab. The ENA is located at the center of area for the transformed section so the computation to locate the ENA is a centroid calculation. Note that you can compute the location of the ENA relative to any location that you like. Some common locations include top of slab, top of top beam flange, center of steel beam, or bottom of bottom steel beam flange. It really doesn't make a difference in the end where your reference is, so long as you are consistent.
| Slab | |||
| n, use | 9 | ||
| ts | 4 | in | |
| bE | 63 | in | |
| bE / n | 7 | in | |
| Section | W18x35 | ||
| d | 17.7 | in | |
| Ix | 510 | in4 | |
| Ag | 10.3 | in2 | |
| Cover Plate | |||
| t | 0.5 | in | |
| b | 4 | in | |
| Find ENA: | |||
| Part | Area | y(top) | yA |
| (in2) | (in) | (in3) | |
| Concrete | 28.0 | 2.00 | 56.0 |
| Beam | 10.3 | 12.85 | 132.4 |
| Cover PL | 2.0 | 21.95 | 43.9 |
| Whole Section | 40.3 | 5.76 | 232.3 |
From this computation we learn that the ENA is located 5.76 inches from the top of the slab.
Once we know where the ENA is located we can now use the parallel axis theorem to compute the transformed moment of inertia. In the following computation, the "y" distances are the distances from the ENA to the centroid of the part.
| Find ITR: | |||||
| Part | Area | y(ENA) | y2A | Io | ITR |
| (in2) | (in) | (in4) | (in4) | (in4) | |
| Concrete | 28.0 | -3.76 | 396.5 | 37.33 | 433.85 |
| Beam | 10.3 | 7.09 | 517.3 | 510.00 | 1027.30 |
| Cover PL | 2.0 | 16.19 | 524.0 | 0.0417 | 524.07 |
| Whole Section | 40.3 | 1985.22 |
The final result is that the transformed moment of inertia about the strong axis (relative to steel stiffness) is 1,985 in4.