| Overview |
| Equivalent Stiffness |
| Transformed Moment of Interia, ITR |
| Example Problems |
| Homework Problems |
| Report Errors or Make Suggestions |
Section ITR.3
Transformed Moment of Inertia
Last Revised: 11/04/2014
A Moment of Inertia, I, is a section property (i.e. solely depended on cross sectional dimensions) taken about a specific axis. The general equation for I is:
I = ∫ y2dA
Figure ITR.3.1
General Moment of Inertia
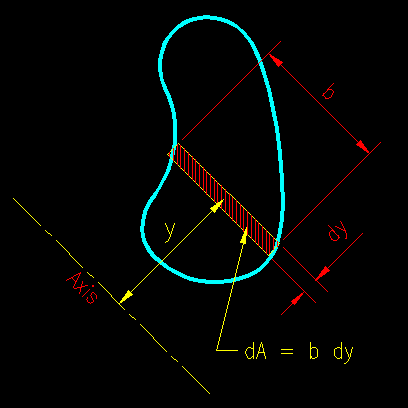
For the case shown in Figure ITR.3.1, the differential area becomes:
dA = b(y) dy
So that the general equation becomes:
I = ∫ b(y) y2dy
For the special case where b(y) is a constant the equation for moment of inertia becomes:
I = b ∫ y2dy
For this case, we see that moment of inertia is linear with respect to dimensions that are parallel to the axis about which I is being determined.
The computation of I assumes a homogeneous material. If a section made of more than one material, each with a different stiffness, E, then the section needs to be transformed into an equivalent section in one material. In this case, equivalent means that the transformed section would result in a moment of inertia that yields that same defection results in elastic deformation equations as the composite section does by other means.
So, given the derivation above, the key to transforming a section into a homogeneous material is to only change those dimensions that are parallel to the reference axis.
As previously shown, an area with equivalent stiffness is found as
A1 = n A2
For a differential rectangle:
b1 dy = n b2 dy
b1 = n b2
Where n is the ratio of E2/E1. Following convention, E2 would be the stiffer material and E1 the less stiff and the equation above would be transforming a stiff material into a less stiff material, so:
bless stiff = n bstiffer
To go the other way you get:
bstiffer = bless stiff / n
Probably the best way to show this is by example.
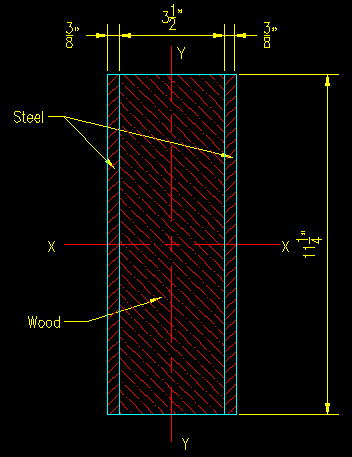
Example #1: Composite Wood & Steel
|
Figure ITR.3.2 |
|
|
For the section shown in Figure ITR.3.2, the steel and wood are bonded together in such a way that they act as a composite section. This section is fairly easy to deal with since it is doubly symmetric and will remain so after the transformations.
Use Es = 29 x 106 psi and Ew = 1.4 x 106 psi. The steel is the stiffer material.
n = 29/1.4 = 20.7 ... use n = 20.5
There are several routes that we can go here.
First, let's find Ixtr and Iytr when converting the wood into steel:
First Ixtr,s. Transform the wood dimension parallel to the "x" axis to an equivalent width:
bw,s = 3.5" / 20.5 = 0.171 inches
The total width of the transformed-to-steel section is now
btotal,s = 0.375" + 0.171" + 0.375" = 0.921"
The resulting steel section is shown in Figure ITR.3.3a.
Since the section is a rectangle centered on the x axis, we can compute:
Ixtr,s = (0.921") (11.25")3 / 12 = 109.2 in4
Next Iytr,s: Transform the wood dimension parallel to the "y" axis to an equivalent
|
Figure ITR.3.3 |
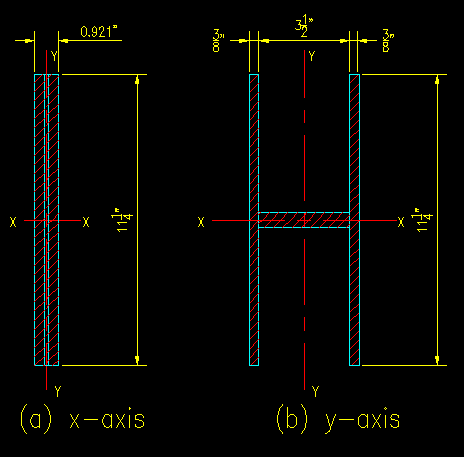 |
width:
bw,s = 11.25" / 20.5 = 0.549 inches
The transformed section is shown in Figure ITR3.3b. There are a couple of ways that you could compute Iytr from this section. Here is one:
Iytr,s = (11.25") (4.25")3 / 12 - (11.25" - .549") (3.5")3 / 12 = 33.73 in4
These moments of inertia would be used in conjunction with Es in deflection equations. Stresses computed on the section would be accurate for the steel, but would needed to be modified by the factor n for the wood.
Now, let's convert the wood to equivalent wood.
For Ixtr,s we have an new width for each plate:
bs,w = (0.375") (20.5) = 7.69"
for a total transformed section width of
btotal,w = 7.69" + 3.5" + 7.69" = 18.88"
The transformed section is shown in Figure ITR.3.4a.
Figure ITR.3.4
Equivalent Wood Sections
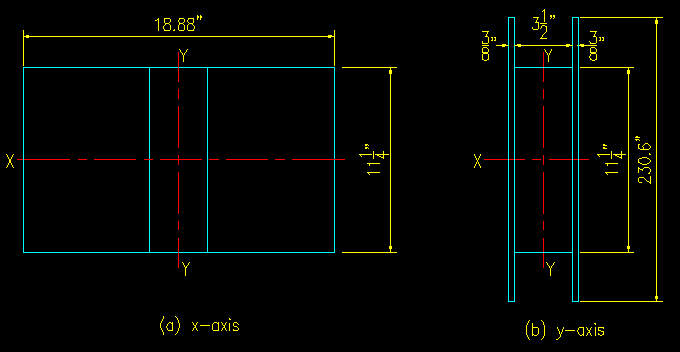
Ixtr,w = (18.88") (11.25")3 / 12 = 2,240 in4
To compute Iytr,w we need to multiply the height dimension of the steel plates by n.
bs,w = (11.25") (20.5) = 230.6 in
The transformed section is shown in Figure ITR.3.4b.
The result is:
Iytr,w = (230.6") (4.25")3 /12 - (230.6" - 11.25") (3.5")3 / 12 = 691.5 in4
A check on the results should show that EI is approximately the same in both cases:
About the x axis
Es Ixtr,s = (29x106 psi) (109.2 in4) ~ Ew Ixtr,w = (1.4x106 psi) (2240 in4)
3.167x109 lb-in2 ~ 3.136x109 lb-in2
The difference in the result (about 1%) is the result of the rounding on the value for n and is close enough, in most cases, for what we do as engineers. A similar result is found if you compare Es Iytr,s and Ew Iytr,w.