|
|
|
|
|
|
|
|
|
|
|
Section 8.3.1
Shear Behavior
Last Revised: 07/30/2011
Shear strength is a potentially limiting criteria for steel members. It must be investigated where a member is subjected to shear. Understanding the behavior of steel members subject to shear will help you understand the SCM approach to ensuring that steel members have adequate shear strength.
Shear Stress Distribution
Internal shear force varies along the length of most bending members. The determination of the magnitude of internal shear at any given location is determined using principles of statics. A common approach is to develop a shear diagram (i.e. a graph of internal shear force over the member length) to show how shear varies.
The distribution of elastic beam shear stress on a given cross section is determined by the following equation as derived in mechanics.
t = VQ/(Ib)
Where:
- is the shear stress at some point on the cross section.
- V is the shear force acting on the cross section.
- Q is the first moment of area “above” the point where of interest is. See any mechanics text for computation of this value.
- I is the moment of inertia of the cross section.
- b is the breadth (i.e. width), parallel to the axis of bending, of the cross section at the point of interest.
The graph of this equation over the height of a rectangular section and an "I" shaped section is shown in Figure 8.3.1.1.
Figure 8.3.1.1
Shear Stress Distribution
Click on image for larger view
As can be seen for an I-shaped member, when the bending member is loaded in the plane of the web as shown in Figure 8.3.1.1, the shear stress is prominent in the web and not the flanges of the member. Hence, the web is designed to carry the shear forces in this case.
When an I-shaped bending member is loaded perpendicular to the web, the shear forces are carried by stresses in the flanges which act as a pair of rectangular sections. The maximum shear stress in this case equals 1.5 V/Af.
Comparing the magnitudes of the shearing stresses, note that the peak shear stress in a rectangular section (for example, the flanges of an I-shaped member loaded perpendicular to the web) is 1.5 times the average shear stress (V/A). In an I-shaped member loaded in the plane of the web, the peak shear stress is nearer to the average shear stress. Consequently, we will find in the SCM different requirements for each plane of bending for I shaped members.
The Effects of Plate Slenderness
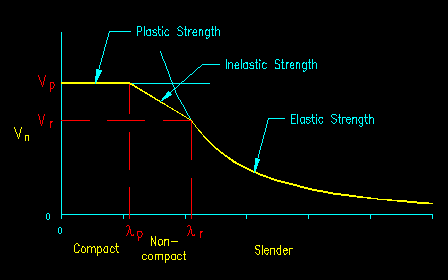
In many steel shapes, the web can be quite slender, leading to shear buckling. As we saw in the section on plate buckling when subjected to normal compressive stress, there are the three regions of behavior: plastic, inelastic buckling, and slender (Euler) buckling. Similar regions are experienced with plate shear buckling.
A simple experiment with heavy paper (card stock is good!) will illustrate for you what plate shear buckling looks like. Hold opposing sides and apply a shear force. The sheet will buckle out of plane and at an angle that is approximately 45 degrees from the direction of applied shear. This propensity to buckle is a function of the thickness of the plate and dimensions of the shear panel.
Figure 8.3.1.3 shows a typical strength curve based on slenderness.
Figure 8.3.1.3
Shear Strength as a Function of Plate Slenderness
The Effect of Stiffening Shear Panels
Shear strength can be improved by adding plate stiffeners to prevent out-of-plane buckling of the web. These stiffeners can be spaced to reduce the shear panel dimensions so that failure is plastic deformation instead of elastic buckling. Figure 8.3.1.3 shows how these stiffeners are arranged.
Figure 8.3.1.3
Transverse Web Stiffeners
Click on hotlinks in image for larger views
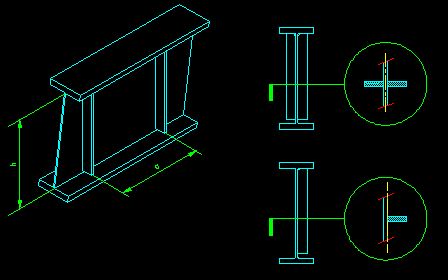
The specification includes provisions for strengthening of shear panels with stiffeners. SCM G2.2 requires that the moment of inertia about an axis centered in the beam web meet certain criteria. The moment of inertia of the stiffeners (the shaded areas in Figure 8.3.1.3) is computed about the axis shown in yellow on the section drawing. You can click on the sub-sections of Figure 8.3.1.3 to get larger views of each stiffener area. We go into more detail on the design of these elements in a later section.
