|
|
|
|
|
|
|
|
|
|
|
Section 8.6.4
Bearing Plate Design
Last Revised: 07/30/2011
Bearing plates are used to transfer concentrated compressive forces between two structural elements. Typically this occurs in two conditions:
- When a beam or column is supported by concrete or masonry, or
- When a beam supports are large concentrated load from a supported element, such as a column.
The next three sections look at these conditions:
|
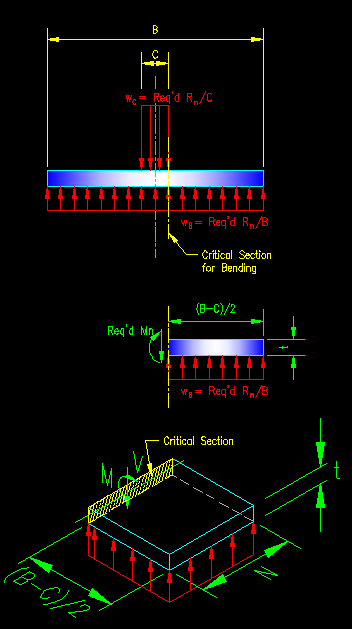
Figure 8.6.4.1 |
|
|
A bearing plate is generally modeled as a double cantilevered beam as shown in Figure 8.6.4.1. The force that is transferred is distributed over the two bearing lengths B and C. The resulting distributed loads are shown.
The second image in Figure 8.6.4.1 is a free body diagram of the base plate cut at the location of critical moment in the base plate. This moment is resisted by the critical section shown in the third image of Figure 8.6.4.1.
The challenge is to select the three defining variables: N, B, and t.
The dimensions N and B will be determined using limit states that are a function of the type of bearing plate being used.
The thickness of the bearing plate is found simply by considering the flexural yielding limit state:
Req'd Mn < Actual Mn = Fy Z
Since the load is a uniformly distributed load on a cantilever
Req'd Mn = (Req'd Rn/B) ((B-C)/2)2 / 2
Since the critical section for bending is a rectangle:
Z = Nt2/4
Substituting this equations for Req'd Mn and Z into the flexural yielding limit state equation and solving for t results in the equation:
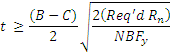
Notice that the term (B-C)/2 is the length of the cantilever.
Also note that, in some cases, it is common to perform this calculation in two orthogonal directions if the bearing plate extends in two directions from the supported member.
The following sections describe the particulars on computing N and B for some common cases of bearing plate design.
<<< Previous Section <<< >>> Next Section >>>