|
Limit State of Flexural Buckling for Compact and Non-compact Sections |
|
|
Section 7.3
Limit State of Flexural Buckling for Compact and Non-compact Sections
Last Revised: 11/04/2014
The flexural buckling strength for compact and non-compact sections (i.e. those sections that do not have slender elements as defined by SCM B4) limit state is found in SCM E3. See the commentary on SCM page 16.1-292 for more discussion on this.
Since this limit state only applies for compact and non-compact sections, the SCM B4 criteria must be checked to make sure that the chosen section is not slender before applying this limit state.
The Limit State
The basic limit state follows the standard form. The statement of the limit states and the associated reduction factor and factor of safety are given here:
| LRFD | ASD |
| Pu < fcPn | Pa < Pn/Wc |
| Req'd Pn = Pu / fc < Pn | Req'd Pn = Pu Wc < Pn |
| Pu / (fcPn) < 1.00 | Pa / (Pn/Wc) < 1.00 |
| fc = 0.90 | Wc = 1.67 |
The values of Pu and Pa are the LRFD and ASD factored loads, respectively, applied to the column.
In this case, Pn is the nominal compressive strength of the member is computed using SCM equation E3-1:
Pn = FcrAg
Where:
- Fcr is the flexural buckling stress.
- Ag is the gross cross sectional area of the member.
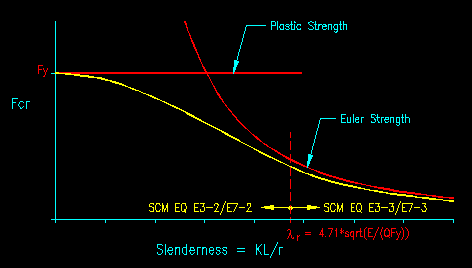
The SCM has two formulas for determining the flexural buckling stress. The first equation, E3-2, covers both the plastic and inelastic buckling regions of the typical buckling strength curve as shown in Figure 6.1.3. The second equation, E3-3, covers the slender region. Figure 7.3.1 shows how the SCM equations for Fcr vary with slenderness.
Figure 7.3.1
Fcr vs. Slenderness
Click on image for larger view
The criteria for selecting which formula to use is based on either the slenderness ratio for the member or the relationship between the Euler buckling stress and the yield stress of the material. The selection, as found in SCM E3, can be stated as:
if (KL/r < 4.71*sqrt(E/Fy)) or (Fy / Fe < 2.25) then
use SCM Equation E3-2
else
use SCM Equation E3-3
The equations require you to compute the theoretical Euler buckling stress, Fe, for the member. This can be done by using SCM equation E3-4 or by more advanced methods of elastic buckling analysis. The other advanced methods for computing Fe are not covered in this text.
The effective length coefficient, K is taken as 1.00 for all purposes of this section if the demand side of the inequality (i.e. Pu or Pa) was determined using the Direct Analysis method, otherwise use the K computed using methods in SCM Appendix 7.
Sample Spreadsheet Calculation
The following spreadsheet example computes the nominal capacity of a W section column according to the requirements of SCM E3. Note that the value of KL is given. This may have resulted from either a Direct Analysis or Effective Length Analysis--the method is not shown. The values in shaded cells were computed before reaching this point.
| W10X19 | Fy = | 50 | ksi | |||||
| A992 | ||||||||
| Check Local Buckling Criteria: SCM Table B4.1 | ||||||||
| Case | Coeff. | Ratio | Actual | Limit | Act/Limit | |||
| 3 | 0.56 | bf/2tf | 5.09 | 13.49 | 0.377 | Not Slender | ||
| 10 | 1.49 | h/tw | 35.4 | 35.88 | 0.987 | Not Slender | ||
| Use SCM E3 | ||||||||
| Compute Global Slenderness Values | ||||||||
| Direction | KL | r | KL/r | |||||
| (ft) | (in) | |||||||
| Stong | 30 | 4.14 | 86.96 | <--- Controlling Value | ||||
| Weak | 6 | 0.874 | 82.38 | |||||
| Determine Pn | ||||||||
| Determine SCM E3 formula to use | ||||||||
| 4.71sqrt(E/Fy) | 113.43 | |||||||
| Controlling KL/r | 86.96 | |||||||
| (KL/r)/limit | 0.767 | … Use SCM Equation E3-2 | ||||||
| Fe | 37.85 | ksi | ||||||
| Fcr | 28.76 | ksi | ||||||
| Ag | 5.62 | in^2 | ||||||
| Pn | 161.66 | kips | ||||||
| LRFD | ASD | |||||||
| fc = | 0.9 | Wc = | 1.67 | |||||
| Pu < | 145.5 | kips | Pa < | 96.8 | kips | |||
| CLF | 1.311 | CLF | 0.806 | |||||
| Ps,eq < | 110.97 | kips/connection | Ps,eq < | 120.17 | kips/connection | |||